A scalene triangle has no congruent sides and no congruent angles. That is to say a scalene triangle has no sides or angles which are the same.
For more...
Monday, April 20, 2009
Sunday, April 19, 2009
Multiplying decimals
When multiplying decimals:
1. Ignore the decimal point
2. Add the number of digits to the right of the point of the numbers you are multiplying
3. Starting from the right of the answer, place that number of digits before the decimal point (add zeros if you have to)
Example:
.2 * .4
1. Ignore digits so 2*4 = 8
2. Count numbers 1 and 1, so 2 total
3. Count over two from right of answer so 0.08
Now
0.03 * 0.004
1. Ignore digits: 3*4 = 12
2. Count digits: 2 and 3 so 5 total
3. Count over: 0.00012
also 1.33 * 3.44
1. Ignore digits so 133*344 = 45752
2. Count: 2 and 2 so 4
3. Count over: 4.5752
Nice!
1. Ignore the decimal point
2. Add the number of digits to the right of the point of the numbers you are multiplying
3. Starting from the right of the answer, place that number of digits before the decimal point (add zeros if you have to)
Example:
.2 * .4
1. Ignore digits so 2*4 = 8
2. Count numbers 1 and 1, so 2 total
3. Count over two from right of answer so 0.08
Now
0.03 * 0.004
1. Ignore digits: 3*4 = 12
2. Count digits: 2 and 3 so 5 total
3. Count over: 0.00012
also 1.33 * 3.44
1. Ignore digits so 133*344 = 45752
2. Count: 2 and 2 so 4
3. Count over: 4.5752
Nice!
Saturday, April 18, 2009
Topology
Topology (Greek Τοπολογία, from τόπος, “place”, and λόγος, “study”) is a major area of mathematics that has emerged through the development of concepts from geometry and set theory, such as those of space, dimension, shape, transformation and others.
Ideas that are now classified as topological were expressed as early as 1736, and toward the end of the 19th century a distinct discipline developed, called in Latin the geometria situs (“geometry of place”) or analysis situs (Greek-Latin for “picking apart of place”), and later gaining the modern name of topology. In the middle of the 20th century, this was an important growth area within mathematics.
The word topology is used both for the mathematical discipline and for a family of sets with certain properties that are used to define a topological space, a basic object of topology. Of particular importance are homeomorphisms, which can be defined as continuous functions with a continuous inverse. For instance, the function y = x3 is a homeomorphism of the real line.
Topology includes many subfields. The most basic and traditional division within topology is point-set topology, which establishes the foundational aspects of topology and investigates concepts as compactness and connectedness; algebraic topology, which generally tries to measure degrees of connectivity using algebraic constructs such as homotopy groups and homology; and geometric topology, which primarily studies manifolds and their embeddings (placements) in other manifolds. Some of the most active areas, such as low dimensional topology and graph theory, do not fit neatly in this division.
http://en.wikipedia.org/wiki/Topology
Ideas that are now classified as topological were expressed as early as 1736, and toward the end of the 19th century a distinct discipline developed, called in Latin the geometria situs (“geometry of place”) or analysis situs (Greek-Latin for “picking apart of place”), and later gaining the modern name of topology. In the middle of the 20th century, this was an important growth area within mathematics.
The word topology is used both for the mathematical discipline and for a family of sets with certain properties that are used to define a topological space, a basic object of topology. Of particular importance are homeomorphisms, which can be defined as continuous functions with a continuous inverse. For instance, the function y = x3 is a homeomorphism of the real line.
Topology includes many subfields. The most basic and traditional division within topology is point-set topology, which establishes the foundational aspects of topology and investigates concepts as compactness and connectedness; algebraic topology, which generally tries to measure degrees of connectivity using algebraic constructs such as homotopy groups and homology; and geometric topology, which primarily studies manifolds and their embeddings (placements) in other manifolds. Some of the most active areas, such as low dimensional topology and graph theory, do not fit neatly in this division.
http://en.wikipedia.org/wiki/Topology
Friday, April 17, 2009
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a number of events occurring in a fixed period of time if these events occur with a known average rate and independently of the time since the last event. The Poisson distribution can also be used for the number of events in other specified intervals such as distance, area or volume.
http://en.wikipedia.org/wiki/Poisson_distribution
http://en.wikipedia.org/wiki/Poisson_distribution
Thursday, April 16, 2009
Radix and Base
In arithmetic, the radix or base refers to the number b in an expression of the form bn. The number n is called the exponent and the expression is known formally as exponentiation of b by n or the exponential of n with base b. It is more commonly expressed as "the nth power of b", "b to the nth power" or "b to the power n". The term power strictly refers to the entire expression, but is sometimes used to refer to the exponent.
http://en.wikipedia.org/wiki/Base_(mathematics)
http://en.wikipedia.org/wiki/Base_(mathematics)
Wednesday, April 15, 2009
Sexagesimal
Sexagesimal (base-sixty) is a numeral system with sixty as the base. It originated with the ancient Sumerians in the 2000s BC, was transmitted to the Babylonians, and is still used—in modified form—for measuring time, angles, and geographic coordinates.
The number 60 has twelve factors, 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60, of which 2, 3, and 5 are prime. With so many factors, many fractions of sexagesimal numbers are simple. For example, an hour can be divided evenly into segments of 30 minutes, 20 minutes, 15 minutes, etc. 60 is the smallest number divisible by every number from 1 to 6.
http://en.wikipedia.org/wiki/Sexagesimal
The number 60 has twelve factors, 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60, of which 2, 3, and 5 are prime. With so many factors, many fractions of sexagesimal numbers are simple. For example, an hour can be divided evenly into segments of 30 minutes, 20 minutes, 15 minutes, etc. 60 is the smallest number divisible by every number from 1 to 6.
http://en.wikipedia.org/wiki/Sexagesimal
Tuesday, April 14, 2009
Decimals
Decimal notation is the writing of numbers in a base-10 numeral system. Examples are Roman numerals, Brahmi numerals, and Chinese numerals, as well as the Arabic numerals used by speakers of English. Roman numerals have symbols for the decimal powers (1, 10, 100, 1000) and secondary symbols for half these values (5, 50, 500). Brahmi numerals had symbols for the nine numbers 1–9, the nine decades 10–90, plus a symbol for 100 and another for 1000. Chinese has symbols for 1–9, and fourteen additional symbols for higher powers of 10, which in modern usage reach 1044.
http://en.wikipedia.org/wiki/Decimal
http://en.wikipedia.org/wiki/Decimal
Monday, April 13, 2009
Proper and Improper Fractions
I had almost forgot about this distinction.
Proper fractions always have a smaller number in the numerator than in the denominator. (On top than under)
Examples of proper fractions
1/2 , 2/5 , 6/17
Improper fractions have a larger numerator than denominator like
5/2 , 7/4 , 20/17
These fractions can be rewritten with whole numbers included like
5/2 = 2(1/2)
7/4 = 1(3/4)
20/17=1(3/17)
Proper fractions always have a smaller number in the numerator than in the denominator. (On top than under)
Examples of proper fractions
1/2 , 2/5 , 6/17
Improper fractions have a larger numerator than denominator like
5/2 , 7/4 , 20/17
These fractions can be rewritten with whole numbers included like
5/2 = 2(1/2)
7/4 = 1(3/4)
20/17=1(3/17)
Sunday, April 12, 2009
The Golden Ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio between the sum of those quantities and the larger one is the same as the ratio between the larger one and the smaller. The golden ratio is an irrational mathematical constant, approximately 1.6180339887.
http://en.wikipedia.org/wiki/Golden_ratio
http://en.wikipedia.org/wiki/Golden_ratio
Saturday, April 11, 2009
The Quadratic Formula
The quadratic formula can help you solve any quadratic equation of the form
ax2 + bx + c
To find the solutions to this equation we can use the quadratic formula which is written as follows
(-b (+or-) sqrt(b2-4ac)) / 2a
Let us consider an example of
x2 + 6x + 7
a=1
b=6
c=7
so
(-6 (+or-) sqrt(62-4*1*7)) / 2*1
=
-6 (+or-) sqrt(36 - 28) / 2
=
-6 (+or-) sqrt(8) / 2
We can simplify the square root so we get
(-6 (+or-) 2sqrt(2)) / 2
=
-3 +or- sqrt(2)
and that is our final answer.
ax2 + bx + c
To find the solutions to this equation we can use the quadratic formula which is written as follows
(-b (+or-) sqrt(b2-4ac)) / 2a
Let us consider an example of
x2 + 6x + 7
a=1
b=6
c=7
so
(-6 (+or-) sqrt(62-4*1*7)) / 2*1
=
-6 (+or-) sqrt(36 - 28) / 2
=
-6 (+or-) sqrt(8) / 2
We can simplify the square root so we get
(-6 (+or-) 2sqrt(2)) / 2
=
-3 +or- sqrt(2)
and that is our final answer.
Friday, April 10, 2009
Solving Equations with a Square Root
When we solve an equation by taking a square root, we have to consider both a positive and negative outcome.
For example consider -3 and 3
now 32 = 9 and -32=9
Thus when we have an equation such that
x2 = 9 to find x we need to take the square root of 9, however, then we have to say x= + or - 3 that is to say positive or negative 3 since it could be either and we don't know.
For example consider -3 and 3
now 32 = 9 and -32=9
Thus when we have an equation such that
x2 = 9 to find x we need to take the square root of 9, however, then we have to say x= + or - 3 that is to say positive or negative 3 since it could be either and we don't know.
Thursday, April 9, 2009
Multiplying and dividing square roots (radicals)
Square roots act just like other numbers when you multiply and divide them, consider the example
3sqrt(5) * 5sqrt(6) = 15sqrt(30)
Similarly
15sqrt(30) / 5sqrt(6) = 3sqrt(5)
3sqrt(5) * 5sqrt(6) = 15sqrt(30)
Similarly
15sqrt(30) / 5sqrt(6) = 3sqrt(5)
Wednesday, April 8, 2009
Adding and Subtracting Radicals
When adding and subtracting radicals you treat the radicands as variables.
Example
3sqrt(5) + 4sqrt(5) = 7sqrt(5)
However, we cannot add together a radicand that is different as in
3sqrt(5) + 4sqrt(2)
Example
3sqrt(5) + 4sqrt(5) = 7sqrt(5)
However, we cannot add together a radicand that is different as in
3sqrt(5) + 4sqrt(2)
Labels:
adding,
algebra,
radicals,
square root,
subtracting
Tuesday, April 7, 2009
The square root of a fraction
By definition we cannot derive the square root of a fraction. Thus we must find a way to get a fraction out of the radical.
Consider the square root of 1/2
sqrt(1/2)
how can we get the fraction out? We have to multiply and make the denominator a perfect square. But what we multiply to the bottom we must also multiply to the top
sqrt((1/2)*(2/2))
=
1/2*sqrt(2)
Now we have got the fraction out of the radical and created a square root we can rationalize.
Another example
sqrt(3/5)
To get the denominator out we multiply by (5/5) (which is equal to 1)
sqrt((3/5)*(5/5))
=
(1/5)*sqrt(3*5)
=
(1/5)*sqrt(15)
Consider the square root of 1/2
sqrt(1/2)
how can we get the fraction out? We have to multiply and make the denominator a perfect square. But what we multiply to the bottom we must also multiply to the top
sqrt((1/2)*(2/2))
=
1/2*sqrt(2)
Now we have got the fraction out of the radical and created a square root we can rationalize.
Another example
sqrt(3/5)
To get the denominator out we multiply by (5/5) (which is equal to 1)
sqrt((3/5)*(5/5))
=
(1/5)*sqrt(3*5)
=
(1/5)*sqrt(15)
Monday, April 6, 2009
Simplifying Radicals
Like so much of algebra, it is good to know how to simplify radicals for purposes of canceling out or combining like terms.
Consider the square root of 27 or sqrt(27) there is no whole number that equals sqrt(27) but we can write the radical as sqrt(9*3) and that is equal to 3*sqrt(3)
Thus we have simplified the radical for purposes of mathematical calculation or canceling.
Consider the square root of 27 or sqrt(27) there is no whole number that equals sqrt(27) but we can write the radical as sqrt(9*3) and that is equal to 3*sqrt(3)
Thus we have simplified the radical for purposes of mathematical calculation or canceling.
Sunday, April 5, 2009
Square roots are radical
It is true, taking the square root of an expression can also be called "The radical"
We will write square root as sqrt on this website, thus
sqrt(4) = 2
and
sqrt(9x2y10) ?
To solve this, it is good to factor under the radical ( or factor the square root)
So we get
sqrt(9x2y10)
=
(3xy5)
We will write square root as sqrt on this website, thus
sqrt(4) = 2
and
sqrt(9x2y10) ?
To solve this, it is good to factor under the radical ( or factor the square root)
So we get
sqrt(9x2y10)
=
(3xy5)
Saturday, April 4, 2009
Solving quadractics by factoring
One way to solve a quadratic equation like:
(4x2 - 4)=0 is by factoring and setting both factors equal to zero. Because a quadratic contains a x2 they often have two solutions.
(4x2 - 4)=0 can be factored to
(2x - 2)(2x + 2)=0
Now set both factors equal to zero
2x-2=0
2x+2=0
we get
x=1 and x=-1
substituting 1 or -1 for x will solve the quadratic equation (4x2 + 4)=0
(4x2 - 4)=0 is by factoring and setting both factors equal to zero. Because a quadratic contains a x2 they often have two solutions.
(4x2 - 4)=0 can be factored to
(2x - 2)(2x + 2)=0
Now set both factors equal to zero
2x-2=0
2x+2=0
we get
x=1 and x=-1
substituting 1 or -1 for x will solve the quadratic equation (4x2 + 4)=0
Friday, April 3, 2009
Quadratic Equation
A quadratic equation is described as an equation where the highest exponent is 2.
The graph of a quadratic is a smooth curve known as a parabola.
All of the following are quadratic equations.
x2 + 4 = 0
x2 + 4x + 3 = 0
3x2 + 34x + 7 = 50
The graph of a quadratic is a smooth curve known as a parabola.
All of the following are quadratic equations.
x2 + 4 = 0
x2 + 4x + 3 = 0
3x2 + 34x + 7 = 50
Thursday, April 2, 2009
Factoring a trinomial
As I said yesterday, I really think factoring comes down to trial and error till the process is internalized. As an example today we will factor trinomials.
Consider
5x2 - 8x - 21
This is quite a complicated trinomial to factor, lets start with a guess
First off, we know that to get 5x2 we need to multiply 5x and x, so that gives us our first two terms:
(5x + ) (x - )
As a further guess I also alternated the signs.
Now we can try guess what two numbers can multiply to give us -21. How about 7 and -3?
(5x + 7) (x - 3)
Checking with the foil method we get
5x2 - 8x - 21
Consider
5x2 - 8x - 21
This is quite a complicated trinomial to factor, lets start with a guess
First off, we know that to get 5x2 we need to multiply 5x and x, so that gives us our first two terms:
(5x + ) (x - )
As a further guess I also alternated the signs.
Now we can try guess what two numbers can multiply to give us -21. How about 7 and -3?
(5x + 7) (x - 3)
Checking with the foil method we get
5x2 - 8x - 21
Wednesday, April 1, 2009
Factoring with the difference of squares
I think factoring is something which becomes internal, you see a problem, make a guess, and then check. The best method is trial and error till it becomes intuitive.
Still the difference of squares method is often taught, and so I will show it here.
Basically the difference of squares is always factored in the following form:
(x+y)(x-y)
Which equals (x2 - y2)
Example
x2 - 9
9 is a perfect square so we can use the memorized formula
(x-3)(x+3)
Again, I prefer gaining an intuitive understanding of factoring, but memorizing a rule like this can help till you gain an intuitive understanding.
Still the difference of squares method is often taught, and so I will show it here.
Basically the difference of squares is always factored in the following form:
(x+y)(x-y)
Which equals (x2 - y2)
Example
x2 - 9
9 is a perfect square so we can use the memorized formula
(x-3)(x+3)
Again, I prefer gaining an intuitive understanding of factoring, but memorizing a rule like this can help till you gain an intuitive understanding.
Labels:
algebra,
difference of squares,
intuitive,
rule
Tuesday, March 31, 2009
Factoring binomials using the greatest common factor
One way to factor binomials is by searching for the greatest common factor.
Consider
(5x * 25)
In this case the greatest common factor is 5 and the phrase can be written as
5(x*5)
Consider
(5x * 25)
In this case the greatest common factor is 5 and the phrase can be written as
5(x*5)
Monday, March 30, 2009
Multiplying a trinomial by a binomial
Multiplying a trinomial by a binomial is a lot like multiplying a binomial by a binomial. You multiply the first term by all the factors of the second term, then multiply the outer(last) term by all the factors of the second term, then simplify.
Consider the example:
(x+5) (5x2 + 3x + 6)
First we multiply our first term (x) by every term in the trinomial (5x2 + 3x + 6)
this gives us:
(5x3 + 3x2 + 6x)
next we multiply our outer term (5) by every term in the trinomial (5x2 + 3x + 6)
this gives us:
(25x2 + 15x + 30)
so we have
(5x3 + 3x2 + 6x) + (25x2 + 15x + 30)
we can simplify by adding like terms to get:
(5x3 + 28x2 + 21x + 30)
Consider the example:
(x+5) (5x2 + 3x + 6)
First we multiply our first term (x) by every term in the trinomial (5x2 + 3x + 6)
this gives us:
(5x3 + 3x2 + 6x)
next we multiply our outer term (5) by every term in the trinomial (5x2 + 3x + 6)
this gives us:
(25x2 + 15x + 30)
so we have
(5x3 + 3x2 + 6x) + (25x2 + 15x + 30)
we can simplify by adding like terms to get:
(5x3 + 28x2 + 21x + 30)
Sunday, March 29, 2009
Multiplying a binomial by a binomial
The most common way to multiply binomials is what is called the FOIL method
First
Outer
Inner
Last
Let us look at an example
(x+4) (x+1)
These are both binomials, to multiply them we first multiply the first two terms to get x2
Then we still take the first x and multiply it by the outer number: 1, to get x.
So far we have
x2 + x
Now we do the inner number: 4
4 times x is 4x
and finally the last number 4 times 1 is 4
So in total we have
x2 + x + 4x + 4
which can be simplified by combining the like x terms to
x2 + 5x + 4
First
Outer
Inner
Last
Let us look at an example
(x+4) (x+1)
These are both binomials, to multiply them we first multiply the first two terms to get x2
Then we still take the first x and multiply it by the outer number: 1, to get x.
So far we have
x2 + x
Now we do the inner number: 4
4 times x is 4x
and finally the last number 4 times 1 is 4
So in total we have
x2 + x + 4x + 4
which can be simplified by combining the like x terms to
x2 + 5x + 4
Saturday, March 28, 2009
Polynomials
Polynomials can be anything from a single number to a variable to a combination of numbers and variables
Monomials have one term.
Such as... 8x4 , 6 , or 2xy
Binomials have 2 terms which are not like.
Such as... 2wz - 4dt , 4x2 - 3x , 4c - 2d
Trinomials have 3 terms which are not like.
Such as... 4bt - 5yu + 9o , 3x2 - 2x + 9 , 5t + 7y - 8u
Monomials have one term.
Such as... 8x4 , 6 , or 2xy
Binomials have 2 terms which are not like.
Such as... 2wz - 4dt , 4x2 - 3x , 4c - 2d
Trinomials have 3 terms which are not like.
Such as... 4bt - 5yu + 9o , 3x2 - 2x + 9 , 5t + 7y - 8u
Friday, March 27, 2009
Dividing exponents
Yesterday we learned that when you multiply exponents you add the number in the exponent, today we see that when you divide exponent you subtract the number in the exponent.
Consider
x7 / 3
What is this equal to?
x*x*x*x*x*x*x / x*x*x = x*x*x*x or x4
x7 / 3 = x7-3 = x4
what about
x3 / 7
= 1 / x7-3 = 1 / x4
We take the reciprocal because the exponent is greater in the divisor, or denominator.
Consider
x7 / 3
What is this equal to?
x*x*x*x*x*x*x / x*x*x = x*x*x*x or x4
x7 / 3 = x7-3 = x4
what about
x3 / 7
= 1 / x7-3 = 1 / x4
We take the reciprocal because the exponent is greater in the divisor, or denominator.
Thursday, March 26, 2009
Exponent
Exponents tell you how many times a factor is multiplied.
x * x * x (x times x times x)
Can be written as x3 or x^3 , when we write the multiplication in this way, we call it an exponent.
To multiply exponents we add them, for example, consider we have
x2 * x3
what is this equal to?
x5
why is this? Well if we write it out, it becomes obvious
x2 * x3
=
(x*x) * (x*x*x) or x5
if we have
5x2 * 2x3
Then the bottom numbers (or base numbers) are multiplied, while the exponents are added
5x2 * 2x3
=
10x5
x * x * x (x times x times x)
Can be written as x3 or x^3 , when we write the multiplication in this way, we call it an exponent.
To multiply exponents we add them, for example, consider we have
x2 * x3
what is this equal to?
x5
why is this? Well if we write it out, it becomes obvious
x2 * x3
=
(x*x) * (x*x*x) or x5
if we have
5x2 * 2x3
Then the bottom numbers (or base numbers) are multiplied, while the exponents are added
5x2 * 2x3
=
10x5
Wednesday, March 25, 2009
Using Substitution to Solve a System of Equations
Suppose we had a system of equations
2x + y = 4
and
3x + 2y = 5
How can we solve for x and y?
The good thing is that we have two equations for two variables.
One way is to solve on equation for y and substitute. Let us start with
2x + y = 4
subtract 2x from both sides
y = 4 - 2x we can use this informaiton to solve for x by substituting y into the other equation
3x + 2y = 5 becomes
3x + 2(4-2x) = 5
3x + 8 - 4x = 5
-x = -3
x=3
so x = 3
Now we can substitute x into our first equation to find y
2x + y = 4
6 + y = 4
y = -2
To check let us substitute our answers into the equations and see if we get the same answer:
2x + y = 4
and
3x + 2y = 5
x=3 y= -2
2(3) - 2 = 4
6-2 =4 Correct.
Next
3(3) + 2(-2) =5
9 - 4 = 5 Correct.
So our solutions to the system check OK and are correct.
2x + y = 4
and
3x + 2y = 5
How can we solve for x and y?
The good thing is that we have two equations for two variables.
One way is to solve on equation for y and substitute. Let us start with
2x + y = 4
subtract 2x from both sides
y = 4 - 2x we can use this informaiton to solve for x by substituting y into the other equation
3x + 2y = 5 becomes
3x + 2(4-2x) = 5
3x + 8 - 4x = 5
-x = -3
x=3
so x = 3
Now we can substitute x into our first equation to find y
2x + y = 4
6 + y = 4
y = -2
To check let us substitute our answers into the equations and see if we get the same answer:
2x + y = 4
and
3x + 2y = 5
x=3 y= -2
2(3) - 2 = 4
6-2 =4 Correct.
Next
3(3) + 2(-2) =5
9 - 4 = 5 Correct.
So our solutions to the system check OK and are correct.
Labels:
algebra,
substitution,
system of linear equations
Tuesday, March 24, 2009
Systems of Linear Equations
A system of linear equations is a composed of two or more equations with the same variables.
If you have two variables then you need two equations
three variables - three equations, and so on.
Let say you have a system of two equations, if you were to graph the two equations
we would say the system has a solution where the two lines intersect.
If the two lines run parallel then there are no solutions.
If the two lines coincide, then they are the same, and there is an infinite number of solutions.
If you have two variables then you need two equations
three variables - three equations, and so on.
Let say you have a system of two equations, if you were to graph the two equations
we would say the system has a solution where the two lines intersect.
If the two lines run parallel then there are no solutions.
If the two lines coincide, then they are the same, and there is an infinite number of solutions.
Monday, March 23, 2009
Linear vs non-linear equations
A linear equation is any equation which graphs a straight line and is of the form
Ax + By = C where A and B are not equal to zero.
examples:
3x + 5y = 8
(4/3)x + 6y = 0
x = 19
These are all linear equations.
Non-linear equations will not be a straight line, and are generally less intuitive, examples are
x^3 + 4y = 8 (this is exponential)
(5/x) + 3y = 9 (contains a variable in the denominator)
2xy = 8 (is multiplicative)
Ax + By = C where A and B are not equal to zero.
examples:
3x + 5y = 8
(4/3)x + 6y = 0
x = 19
These are all linear equations.
Non-linear equations will not be a straight line, and are generally less intuitive, examples are
x^3 + 4y = 8 (this is exponential)
(5/x) + 3y = 9 (contains a variable in the denominator)
2xy = 8 (is multiplicative)
Sunday, March 22, 2009
Solving inequalities
Inequalities are often represented in terms of
less than <
greater than >
and not equal to
I.E.:
3 < 4
4 > 3
4 not equal to 3
Like equalities, they can be solved by manipulating both sides
7 x < 21
divide both sides by 7
x < 3
-----------------
Consider
2 < 4
What if we multiply both sides by -2?
-4 < -8 ...but this is false!
So we must remember with inequalities that when we multiply or divide by a negative number we flip the sign!
-4 > -8 ...now correct!
less than <
greater than >
and not equal to
I.E.:
3 < 4
4 > 3
4 not equal to 3
Like equalities, they can be solved by manipulating both sides
7 x < 21
divide both sides by 7
x < 3
-----------------
Consider
2 < 4
What if we multiply both sides by -2?
-4 < -8 ...but this is false!
So we must remember with inequalities that when we multiply or divide by a negative number we flip the sign!
-4 > -8 ...now correct!
Saturday, March 21, 2009
Graphing linear equations the slope and intercept
Linear equations generally take the form
y = mx + b
m is considered to be the slope of the line
b is the y intercept
The smaller m is, i.e. m = 0.5 or 0.3 the steeper the slope.
y = mx + b
m is considered to be the slope of the line
b is the y intercept
The smaller m is, i.e. m = 0.5 or 0.3 the steeper the slope.
Friday, March 20, 2009
Using formals to find information
Formulas are useful to give us information we may not be able to know otherwise.
Example:
D = rt
where
D = distance
r = rate
t = time
The formula gives us the distance we have traveled accounting for rate and time.
Consider:
We travel 70mph for 7 hours, how far have we gone?
D = 70 * 7 = 490 miles!
Since we know how to simplify expressions and solve for variables we can use the formula to answer many questions.
Consider:
How fast would we have to go to travel 490 miles in 7 hours?
490 = r * 7
r = 490 / 7 = 70 mph
Example:
D = rt
where
D = distance
r = rate
t = time
The formula gives us the distance we have traveled accounting for rate and time.
Consider:
We travel 70mph for 7 hours, how far have we gone?
D = 70 * 7 = 490 miles!
Since we know how to simplify expressions and solve for variables we can use the formula to answer many questions.
Consider:
How fast would we have to go to travel 490 miles in 7 hours?
490 = r * 7
r = 490 / 7 = 70 mph
Thursday, March 19, 2009
Equations of the null and the infinite
Sometimes an equation will resolve to eliminate all its variables, this creates two results
1.Consider
5x + 25 = 5(x-50)
5x + 25 = 5x - 50
we subtract 5x from both sides and get
25=-50 or 0=75
In this case we know the equation doesn't make sense, since 0 is NOT equal to 75. When this happens we say the equation resolves to the empty set and that there is no solution.
2. Consider
5x + 25 = 5(x+5)
5x + 25 = 5x+ 25
we subtract 5x from both sides again
25=25 or 1=1
This solution is called the identity because the left side is exactly equal to the right side. You can substitute any number for x and arrive at the same answer, thus there are an infinite number of solutions. We can say that this equation resolves to the set of all reals, often notated as R.
1.Consider
5x + 25 = 5(x-50)
5x + 25 = 5x - 50
we subtract 5x from both sides and get
25=-50 or 0=75
In this case we know the equation doesn't make sense, since 0 is NOT equal to 75. When this happens we say the equation resolves to the empty set and that there is no solution.
2. Consider
5x + 25 = 5(x+5)
5x + 25 = 5x+ 25
we subtract 5x from both sides again
25=25 or 1=1
This solution is called the identity because the left side is exactly equal to the right side. You can substitute any number for x and arrive at the same answer, thus there are an infinite number of solutions. We can say that this equation resolves to the set of all reals, often notated as R.
Wednesday, March 18, 2009
Equations
Equations are statements that express equalities, typically using an = sign.
Such as
5=5
2+3 = 5
1+1+1+1+1=5
and so on.
Equations are useful because they can allow us to solve for missing variables in any real event we want to model
2x + 1 = 5
2x = 4
x=2
Such as
5=5
2+3 = 5
1+1+1+1+1=5
and so on.
Equations are useful because they can allow us to solve for missing variables in any real event we want to model
2x + 1 = 5
2x = 4
x=2
Tuesday, March 17, 2009
Simplifying Expressions and Combining Like Terms
In Math, like English, there is a desire to reach for simplicity and elegance when making statements.
Be as clear and short as possible to be effective.
Math expressions should be simplified, and one way to do this is to combine like terms, for example, we can realized that
2x + 3x + 2x + 10x = 27x , and it would be much better to write the shorter 27x
However
2x + 3y + 2x + 10y = 4x + 13y and that is as simple as we can get, because not all terms are like. That is to say, y is different from x and cannot be combined.
In the case of parenthesis expressions can be greatly simplified
2(2x + 4y) + 5(10x + 20y)
=
4x + 8y + 50x + 100y
=
54x + 108y
much simpler.
The ability to simplify expressions should not be underestimated. Math is used to model and describe real world problems, and its ability to be simplified allows us to draw insights from the world that would otherwise be obscured in complication.
Be as clear and short as possible to be effective.
Math expressions should be simplified, and one way to do this is to combine like terms, for example, we can realized that
2x + 3x + 2x + 10x = 27x , and it would be much better to write the shorter 27x
However
2x + 3y + 2x + 10y = 4x + 13y and that is as simple as we can get, because not all terms are like. That is to say, y is different from x and cannot be combined.
In the case of parenthesis expressions can be greatly simplified
2(2x + 4y) + 5(10x + 20y)
=
4x + 8y + 50x + 100y
=
54x + 108y
much simpler.
The ability to simplify expressions should not be underestimated. Math is used to model and describe real world problems, and its ability to be simplified allows us to draw insights from the world that would otherwise be obscured in complication.
Monday, March 16, 2009
Which way does the sign go?
The book I am working with makes a big deal about knowing which way the sign goes in operations of addition and subtraction.
I would say just try to work it out logically in your mind
3+4 = 7
3 + -4 = -1
This can get confusing when you subtract a negative number
3 - -4 = 7
This is probably one case where memorization works since it is hard to intuitively see that subtracting a negative number is the same as adding it. So just remember that when you subtract a negative number to just change the sign to addition.
I would say just try to work it out logically in your mind
3+4 = 7
3 + -4 = -1
This can get confusing when you subtract a negative number
3 - -4 = 7
This is probably one case where memorization works since it is hard to intuitively see that subtracting a negative number is the same as adding it. So just remember that when you subtract a negative number to just change the sign to addition.
Sunday, March 15, 2009
Positive and Negative Integers
This blog now begins a series reviewing the basic concepts of algebra.
First we start with the integers, which are a set of whole numbers.
Negative integers are those less than 0
Positive integers are those greater than 0
i.e.
...-3,-2,-1,0,1,2,3...
The sign < means less than
The sign > means greater than
Thus
-3 < 1
3 > 2
3 > -2
and so on.
First we start with the integers, which are a set of whole numbers.
Negative integers are those less than 0
Positive integers are those greater than 0
i.e.
...-3,-2,-1,0,1,2,3...
The sign < means less than
The sign > means greater than
Thus
-3 < 1
3 > 2
3 > -2
and so on.
Saturday, March 14, 2009
Testing for Independence
Suppose we want to know if people who smoke are more likely to get cancer than people who don't smoke.
Such a question requires testing for independence. In this case we are trying to see if the chance of getting cancer is related to smoking.
The test statistic is based on the chi-square distribution and is the same as with tests for homogeneity.
The null hypothesis assumes independence, while the alternative assumes dependence.
Or in other words, the null says that smoking doesn't cause cancer, while the alternative states that smoking does cause cancer.
Often, plotting the data in a table can give a convincing overview, i.e.:
Please note that the data in that table is fictional, and only used for example purposes. Also, please know that presentation of a data in a table, while effective, is not a substitute for statistical testing.
Such a question requires testing for independence. In this case we are trying to see if the chance of getting cancer is related to smoking.
The test statistic is based on the chi-square distribution and is the same as with tests for homogeneity.
The null hypothesis assumes independence, while the alternative assumes dependence.
Or in other words, the null says that smoking doesn't cause cancer, while the alternative states that smoking does cause cancer.
Often, plotting the data in a table can give a convincing overview, i.e.:
| Smoke | |||
| Yes | No | ||
| Cancer | Yes | 68 | 16 |
| No | 9 | 7 |
Please note that the data in that table is fictional, and only used for example purposes. Also, please know that presentation of a data in a table, while effective, is not a substitute for statistical testing.
Friday, March 13, 2009
Test statistic for Homogeneity
In order to test for homogeneity we have to look at the difference of each proportion from the extepected value. For example, looking at income and whether the person rents or owns, we can form some hypothses
at < 30,000 income 30% own homes and 70% rent
at > 80,000 income 70% own homes and 30% rent
Thus we can take our sample and find that
at < 30,000 income 40% own homes and 60% rent
at > 80,000 income 60% own homes and 40% rent
To find our test statistic we take the sum of the actual value from the expected, divided by the expected.
sum across i and sum across j (nij - eij)2 / eij
We use the resultant test statistic and find where it falls on the x-axis of a chi-square distribution. If it falls so that the area to the right and the area above the point is sufficiently less than 0.05 (or our probability tolerance) we assume the data is homogeneous.
at < 30,000 income 30% own homes and 70% rent
at > 80,000 income 70% own homes and 30% rent
Thus we can take our sample and find that
at < 30,000 income 40% own homes and 60% rent
at > 80,000 income 60% own homes and 40% rent
To find our test statistic we take the sum of the actual value from the expected, divided by the expected.
sum across i and sum across j (nij - eij)2 / eij
We use the resultant test statistic and find where it falls on the x-axis of a chi-square distribution. If it falls so that the area to the right and the area above the point is sufficiently less than 0.05 (or our probability tolerance) we assume the data is homogeneous.
Thursday, March 12, 2009
Intro to Tests of Homogeneity
Suppose we wanted to know if the proportions between two populations where similar.
For example:
Are the age ranges between people who rent and people who own homes the same?
Is the income between republican and democratic voters the same?
To answer these questions we have to use tests of homogeneity.
To do this, we take random samples from both groups and record their proportions into categorical variables.
For example:
Are the age ranges between people who rent and people who own homes the same?
Is the income between republican and democratic voters the same?
To answer these questions we have to use tests of homogeneity.
To do this, we take random samples from both groups and record their proportions into categorical variables.
Wednesday, March 11, 2009
Setting Hypothesis for Categorical Data
We looked at setting categorical variables yesterday. Now we look at setting hypothesis for this data.
Suppose are categories are
1 = Those less than 18
2 = Those 18-70
3 = Those 70 or more
and we hypothesize that
p1: 20% are less than 18
p2:70% are 18-70
p3:and 10% are 70 or more
To test this we set
H0 null hypothesis (innocent):
p1: 20% are less than 18
p2:70% are 18-70
p3:and 10% are 70 or more
H1 alternative hypothesis (guilty):
not null (H0)
To test this we would take samples from the population and assess how close the proportions are to our hypothesized values. I.E. how many in our sample are 18 and under and so on....
Then we would calculate "goodness of fit" for how close our sample is to our hypothesis, this can be found by:
X^2 = sum (n(i) - e(i))^2 / e(i)
Where n is estimated proportion from our sample, and e is the expected or hypothesized proportion.
example:
We take a sample of 100 people and find that 25 are under 18 (25%) (we hypothesized 20%)
Thus X^2 = (25-20)^2 / 20 = 5^2 / 20 = 25/20 = 1.25
From this we get the X^2 test statistic which can be used to find the probability of being close enough using the chi-square distribution.
Suppose are categories are
1 = Those less than 18
2 = Those 18-70
3 = Those 70 or more
and we hypothesize that
p1: 20% are less than 18
p2:70% are 18-70
p3:and 10% are 70 or more
To test this we set
H0 null hypothesis (innocent):
p1: 20% are less than 18
p2:70% are 18-70
p3:and 10% are 70 or more
H1 alternative hypothesis (guilty):
not null (H0)
To test this we would take samples from the population and assess how close the proportions are to our hypothesized values. I.E. how many in our sample are 18 and under and so on....
Then we would calculate "goodness of fit" for how close our sample is to our hypothesis, this can be found by:
X^2 = sum (n(i) - e(i))^2 / e(i)
Where n is estimated proportion from our sample, and e is the expected or hypothesized proportion.
example:
We take a sample of 100 people and find that 25 are under 18 (25%) (we hypothesized 20%)
Thus X^2 = (25-20)^2 / 20 = 5^2 / 20 = 25/20 = 1.25
From this we get the X^2 test statistic which can be used to find the probability of being close enough using the chi-square distribution.
Tuesday, March 10, 2009
Categorical Variables
Categorical variables can often show relationships not found in continuous data.
A categorical variable is any discrete variable.
For example:
The probability of a car turning left or right, can be represented as
1 = turns left
2 = turns right
Continuous variables can also be made categorical. For the example of age we may say:
1 = Those less than 18
2 = Those 18-70
3 = Those 70 or more
These three categorical variables should be driven on a hypothesis we want to test for any of those age groups.
How the categories are defined can become an art and so it is good to be cautious when viewing results from categorical data...for example, I may run the test with my current age ranges and find no good result...then I may decide to make
1 = Those less than 24
2 = Those 24-85
3 = Those 85 or more
and find that I now have a great result. Such a change of variable definition to get a good result is not good science. Assumptions should always come first.
A categorical variable is any discrete variable.
For example:
The probability of a car turning left or right, can be represented as
1 = turns left
2 = turns right
Continuous variables can also be made categorical. For the example of age we may say:
1 = Those less than 18
2 = Those 18-70
3 = Those 70 or more
These three categorical variables should be driven on a hypothesis we want to test for any of those age groups.
How the categories are defined can become an art and so it is good to be cautious when viewing results from categorical data...for example, I may run the test with my current age ranges and find no good result...then I may decide to make
1 = Those less than 24
2 = Those 24-85
3 = Those 85 or more
and find that I now have a great result. Such a change of variable definition to get a good result is not good science. Assumptions should always come first.
Monday, March 9, 2009
Hypothesis testing for a sample mean
Testing a sample mean is much like testing a proportion except you use the t-distribution instead of the normal curve, and the t-distribution takes sample size and degrees of freedom into account. Like with the confidence intervals for samples.
Sunday, March 8, 2009
Confidence Intervals for Sample Means
When we find confidence intervals for samples means we use the student-t distribution.
Two conditions must be met: the sample must be random and it the sample size must be large enough for the central limit theorem. (Around 30)
The general formula is:
upper limit: sample mean estimate + t-value*standard error
lower limit: sample mean estimate - t-value*standard error
In math this can be
upper limit: X + t*(s/sqrt(n))
lower limit: X - t*(s/sqrt(n))
The t value is determined by the point on the x-axis that represents the amount of probability we want and is found much like the z-value for proportion confidence intervals.
The t-value must also generally be found by using a computer or a table. The t-distribution takes the number of the sample size into account, and calls this accounting "degrees of freedom". Degrees of freedom are n-1, or one less than your sample size. Generally the more degrees of freedom, the better your estimates.
Two conditions must be met: the sample must be random and it the sample size must be large enough for the central limit theorem. (Around 30)
The general formula is:
upper limit: sample mean estimate + t-value*standard error
lower limit: sample mean estimate - t-value*standard error
In math this can be
upper limit: X + t*(s/sqrt(n))
lower limit: X - t*(s/sqrt(n))
The t value is determined by the point on the x-axis that represents the amount of probability we want and is found much like the z-value for proportion confidence intervals.
The t-value must also generally be found by using a computer or a table. The t-distribution takes the number of the sample size into account, and calls this accounting "degrees of freedom". Degrees of freedom are n-1, or one less than your sample size. Generally the more degrees of freedom, the better your estimates.
Saturday, March 7, 2009
Testing the Hypothesis
The past two days we went over creating a hypothesis and the types of errors that can be made when testing.
Now we will look at testing.
First we make a hypothesis.
Then we take a sample of the population to test the hypothesis.
As with confidence intervals we assume that the sample is random, and that the population is large enough to be normally distributed.
In this way we can use the normal curve to find the probability of our hypothesis being correct. To do this we have to find the point on the x-axis of the normal curve that relates to our data, this is called the Z-statistic.
To find the z-statistic we have to subtract our estimate from our hypothesized value and divide it by the standard error.
Z = (u - u(0)) / H
where u(0) is our hypothesized value
and H is standard error
Once we have our Z statistic we see where it falls on the normal curve, again here are some probabilities associated with particular Z statistics...
90% z=1.645
95% z=1.96
98% z=2.33
99% z=2.58
Most science looks for a Z stat around 2 which gives between a 95-98% chance of making a correct conclusion.
Example.
You like wine, but your friend likes cheese. You hypothesize that more people prefer wine to cheese. You take a random sample of 200 people and find that 57% of people like prefer wine to cheese with a standard error of 3% ... is your hypothesis wrong?
H(O) Null hypothesis: Most people do not prefer wine to cheese
H(1) Alternative hypothesis: Most people prefer wine to cheese
Let us look at the Z statistic
(estimate - hypothesized) / standard error
Z = (57% - 50%) / 3% = 2.3
We get a Z statistic of 2.3 which means you have a 98% chance of being right, that most people prefer wine to cheese.
Now we will look at testing.
First we make a hypothesis.
Then we take a sample of the population to test the hypothesis.
As with confidence intervals we assume that the sample is random, and that the population is large enough to be normally distributed.
In this way we can use the normal curve to find the probability of our hypothesis being correct. To do this we have to find the point on the x-axis of the normal curve that relates to our data, this is called the Z-statistic.

To find the z-statistic we have to subtract our estimate from our hypothesized value and divide it by the standard error.
Z = (u - u(0)) / H
where u(0) is our hypothesized value
and H is standard error
Once we have our Z statistic we see where it falls on the normal curve, again here are some probabilities associated with particular Z statistics...
90% z=1.645
95% z=1.96
98% z=2.33
99% z=2.58
Most science looks for a Z stat around 2 which gives between a 95-98% chance of making a correct conclusion.
Example.
You like wine, but your friend likes cheese. You hypothesize that more people prefer wine to cheese. You take a random sample of 200 people and find that 57% of people like prefer wine to cheese with a standard error of 3% ... is your hypothesis wrong?
H(O) Null hypothesis: Most people do not prefer wine to cheese
H(1) Alternative hypothesis: Most people prefer wine to cheese
Let us look at the Z statistic
(estimate - hypothesized) / standard error
Z = (57% - 50%) / 3% = 2.3
We get a Z statistic of 2.3 which means you have a 98% chance of being right, that most people prefer wine to cheese.
Labels:
hypothesis testing,
statistical testing,
statistics
Friday, March 6, 2009
Type One and Type Two Errors
Yesterday we covered the null and alternative hypothesis, where
the null can be seen as: not guilty
alternative can be seen as: guilty
Because all statistical tests are made with a degree of probability(termed confidence)
there are chances of making errors in our conclusions which can be expressed in two ways:
Type 1 error: Claiming innocence when there is guilt
Type 2 error: Claiming guilt when there is innocence
Example:
Null: IQ doesn't affect school grades
Alternative: IQ affects school grades
Type 1: We conclude IQ does affect grades, when it really doesn't
Type 2: We conclude that IQ does not affect grades, when it really does
There is no need to break your head trying to understand this, just know that whatever conclusion is made from a statistical test, there is always a chance of it being wrong.
As a rule of thumb, science tries to make sure it is correct 1 out of a 100 times. But 1 in 20 and 1 in 10 are also passable.
the null can be seen as: not guilty
alternative can be seen as: guilty
Because all statistical tests are made with a degree of probability(termed confidence)
there are chances of making errors in our conclusions which can be expressed in two ways:
Type 1 error: Claiming innocence when there is guilt
Type 2 error: Claiming guilt when there is innocence
Example:
Null: IQ doesn't affect school grades
Alternative: IQ affects school grades
Type 1: We conclude IQ does affect grades, when it really doesn't
Type 2: We conclude that IQ does not affect grades, when it really does
There is no need to break your head trying to understand this, just know that whatever conclusion is made from a statistical test, there is always a chance of it being wrong.
As a rule of thumb, science tries to make sure it is correct 1 out of a 100 times. But 1 in 20 and 1 in 10 are also passable.
Thursday, March 5, 2009
Hypothesis Testing: The Null and Alternative
What is a hypothesis? Any question that has a cause and effect. Statistics is often used to try answer such questions:
Does IQ relate to school grades?
Does smoking cause cancer?
Do caps protect you from aliens?
All these questions are hypothesis.
To statistically test hypothesis, they must be broken into two parts:
The null hypothesis
The alternative hypothesis
The null hypothesis always asserts the theory is false, while the alternative assumes it is true.
Null: IQ doesn't affect school grades
Alternative: IQ affects school grades
Null: Smoking doesn't cause cancer
Alternative: Smoking causes cancer
Null: Caps do not protect you from aliens
Alternative: Caps protect you from aliens
Null: Not guilty
Alternative: Guilty
Tomorrow we will look at type I and type II errors
Does IQ relate to school grades?
Does smoking cause cancer?
Do caps protect you from aliens?
All these questions are hypothesis.
To statistically test hypothesis, they must be broken into two parts:
The null hypothesis
The alternative hypothesis
The null hypothesis always asserts the theory is false, while the alternative assumes it is true.
Null: IQ doesn't affect school grades
Alternative: IQ affects school grades
Null: Smoking doesn't cause cancer
Alternative: Smoking causes cancer
Null: Caps do not protect you from aliens
Alternative: Caps protect you from aliens
Null: Not guilty
Alternative: Guilty
Tomorrow we will look at type I and type II errors
Labels:
alternative,
hypothesis,
null,
statistical testing,
statistics
Wednesday, March 4, 2009
Confidence Intervals or Margins of Error
Confidence intervals let us express information with a degree of probability.
For example, assume we took a sample survey and found that 80% of the population preferred cheese to wine. We can make a more accurate statement if we say that there is a 95% chance that between 77% and 83% of the population prefers cheese to wine.
This can also be reported as 80% of people prefer cheese to wine with a 3% margin of error.
How do we calculate this?
Well we need three things, the mean(u) the standard error (H) and the Z-statistic from the normal curve (Z)
What is the Z statistic? Well consider the graph below:

Suppose we wanted to find the point on the curve that would include 95% of the area. As this happens it is at the point (2 sigma) and the value of the x axis at this point is 1.96 That is to say when x equals 1.96 we capture 95% of the population under the curve. So the Z statistic equals that point on the x-axis or 1.96
Some other common levels of confidence and Z stats are
90% z=1.645
95% z=1.96
98% z=2.33
99% z=2.58
As you see, the Z statistic gets larger and larger as confidence increases. In other words we can be
95% sure that between 77-83% of people prefer wine to cheese
99% sure that between 76-84% of people prefer wine to cheese
and
100% sure that between 0-100% of people prefer wine to cheese (which isn't really saying anything at all)
Now for our example, the mean is 80% and assume the standard error is 1.5% (pretty small really)
to get our confidence interval we take the mean and add the Z stat times the standard error:
u + Z(H) upper limit
u - Z(H) lower limit
80 + 1.96(1.5) upper limit = 80 + 2.94 = 82.94 or rounded to 83%
80 - 1.96(1.5) lower limit = 80 - 2.94 = 77.06 or rounded to 77%
Thus we say with 95% confidence that the mean(u) is
77% < = u < = 83%
Because the mean is 80% we can find the margin of error by subtracting from the top interval.
83%-80% = 3 percent margin of error. Thus we make the statement 80% of people prefer wine to cheese with a 3% margin of error.
For example, assume we took a sample survey and found that 80% of the population preferred cheese to wine. We can make a more accurate statement if we say that there is a 95% chance that between 77% and 83% of the population prefers cheese to wine.
This can also be reported as 80% of people prefer cheese to wine with a 3% margin of error.
How do we calculate this?
Well we need three things, the mean(u) the standard error (H) and the Z-statistic from the normal curve (Z)
What is the Z statistic? Well consider the graph below:

Suppose we wanted to find the point on the curve that would include 95% of the area. As this happens it is at the point (2 sigma) and the value of the x axis at this point is 1.96 That is to say when x equals 1.96 we capture 95% of the population under the curve. So the Z statistic equals that point on the x-axis or 1.96
Some other common levels of confidence and Z stats are
90% z=1.645
95% z=1.96
98% z=2.33
99% z=2.58
As you see, the Z statistic gets larger and larger as confidence increases. In other words we can be
95% sure that between 77-83% of people prefer wine to cheese
99% sure that between 76-84% of people prefer wine to cheese
and
100% sure that between 0-100% of people prefer wine to cheese (which isn't really saying anything at all)
Now for our example, the mean is 80% and assume the standard error is 1.5% (pretty small really)
to get our confidence interval we take the mean and add the Z stat times the standard error:
u + Z(H) upper limit
u - Z(H) lower limit
80 + 1.96(1.5) upper limit = 80 + 2.94 = 82.94 or rounded to 83%
80 - 1.96(1.5) lower limit = 80 - 2.94 = 77.06 or rounded to 77%
Thus we say with 95% confidence that the mean(u) is
77% < = u < = 83%
Because the mean is 80% we can find the margin of error by subtracting from the top interval.
83%-80% = 3 percent margin of error. Thus we make the statement 80% of people prefer wine to cheese with a 3% margin of error.
Labels:
confidence interval,
margin of error,
probability,
statistics
Tuesday, March 3, 2009
The Central Limit Theorem
The central limit theorem states that if a large enough random sample is drawn from a population then the sampling distribution will be normal.
This could be paraphrased as "All sampling distributions become normal distributions when the sample is large enough" and large enough is generally considered to be 20-30 units.

The normal distribution is everywhere in nature.
This could be paraphrased as "All sampling distributions become normal distributions when the sample is large enough" and large enough is generally considered to be 20-30 units.

The normal distribution is everywhere in nature.
Monday, March 2, 2009
The Law of Large Numbers
In statistics the law of large numbers states that as sample size increases the accuracy of population estimates increases. This is true for all distributions.
Example:
Suppose we had a bag of 100 marbles and wanted to know how many marbles were solid red.
We could start by drawing 10 marbles from the bag and finding that 2 are red. Thus we estimate that 20% are red.
Then we draw 50 marbles and find that 9 are red, thus we now estimate that 18% are red.
Finally, we draw all 100 marbles (census) and find that there are 17 red marbles. Or that 17% of the marbles are red.
In either case, as we drew more and more marbles our estimate got better and better. This is the law of large numbers.
Example:
Suppose we had a bag of 100 marbles and wanted to know how many marbles were solid red.
We could start by drawing 10 marbles from the bag and finding that 2 are red. Thus we estimate that 20% are red.
Then we draw 50 marbles and find that 9 are red, thus we now estimate that 18% are red.
Finally, we draw all 100 marbles (census) and find that there are 17 red marbles. Or that 17% of the marbles are red.
In either case, as we drew more and more marbles our estimate got better and better. This is the law of large numbers.
Sunday, March 1, 2009
Sample Means and Deviations
For any random sample (of size n) taken from a population with mean u and standard deviation H
we can say that the mean is equal to X and that the standard deviation is equal to H/sqrt(n)
That is to say, that as the sample (n) gets larger the estimate of the standard deviation will become smaller and more accurate.
Distributions of sample populations are represented by the "t-distribution" that varies in shape by sample size, and looks much like the normal curve covered earlier. As the sample size approaches the population size the t-distribution looks more and more like the normal curve, but that is tomorrow's lesson.
we can say that the mean is equal to X and that the standard deviation is equal to H/sqrt(n)
That is to say, that as the sample (n) gets larger the estimate of the standard deviation will become smaller and more accurate.
Distributions of sample populations are represented by the "t-distribution" that varies in shape by sample size, and looks much like the normal curve covered earlier. As the sample size approaches the population size the t-distribution looks more and more like the normal curve, but that is tomorrow's lesson.
Labels:
probability,
sample deviation,
sample mean,
statistics,
t-distributon
Saturday, February 28, 2009
The Fine Lines between Parameters and Statistics
When looking at data
parameters are consider to be measures of the whole population that are fixed, but cannot really be known
statistics are considered to be measures of samples from the population that can be known but can vary and are always inaccurate. The amount of inaccuracy is measured, but even these measures are inaccurate, so probabilities of being correct are often stated, along with possible margins of error
For example, if we stop and randomly ask 100 people their age we might find the average to be 40 years old. This is a statistic because it describes a sample.
However, if we look at the census data for the U.S. we find that the average age is in fact 38. This is a parameter because it theoretically describes the whole population.
parameters are consider to be measures of the whole population that are fixed, but cannot really be known
statistics are considered to be measures of samples from the population that can be known but can vary and are always inaccurate. The amount of inaccuracy is measured, but even these measures are inaccurate, so probabilities of being correct are often stated, along with possible margins of error
For example, if we stop and randomly ask 100 people their age we might find the average to be 40 years old. This is a statistic because it describes a sample.
However, if we look at the census data for the U.S. we find that the average age is in fact 38. This is a parameter because it theoretically describes the whole population.
Friday, February 27, 2009
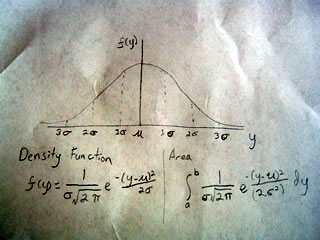
The Normal Distribution (also Gaussian distribution and bell curve)
The Normal distribution is a curve that is symmetric on both sides and centered around the mean of a population. Like all density functions its area under the curve is between 0 and 1.

Here the mean is represented by mu, which looks like u and the standard deviation is measured by sigma, which looks like a flat 6.
The chances of being 1 deviation away from the mean are around 30%, 2 deviations is 5%, and 3 deviations is 1%
Like we covered yesterday the probability of values being between any point a and b can be found by taking the area under the curve at those points. The functions are there in the image, and as you can see, they are not fun to evaluate. Thus tables or computers are typically used to help obtain values as opposed to direct calculation.
The curve is also called the Gaussian curve in honor of Carl Friedrich Gauss, the German mathematician who found it. Another name is "Bell curve" since its shape represents a bell.

Here the mean is represented by mu, which looks like u and the standard deviation is measured by sigma, which looks like a flat 6.
The chances of being 1 deviation away from the mean are around 30%, 2 deviations is 5%, and 3 deviations is 1%
Like we covered yesterday the probability of values being between any point a and b can be found by taking the area under the curve at those points. The functions are there in the image, and as you can see, they are not fun to evaluate. Thus tables or computers are typically used to help obtain values as opposed to direct calculation.
The curve is also called the Gaussian curve in honor of Carl Friedrich Gauss, the German mathematician who found it. Another name is "Bell curve" since its shape represents a bell.
Labels:
bell curve,
gauss,
normal curve,
probability,
statistics
Thursday, February 26, 2009
Continuous Probability Distributions
So far we have looked at discrete probability distributions where values can be assigned to every outcome in the sample space.
For continuous distributions, probability is represented as a function called the probability density function, or density function. These functions must be greater than zero, and must not have an area greater than 1 under their curves. The functions are called "density functions" because they will graph a smooth curve showing values that are most likely or "dense".
Look at the example below which shows a normal curve:

We can see very quickly that observations are most "dense" between 40 and 50. To find out the exact probability of a value being between 40 and 50, we must calculate the area of the region between 40 and 50. The same is true to find the probability of a value being less than 40. We must calculate the area under the curve that is less than 40. Thus we calculate the area under the curve for any probabilities we want to find.
For continuous distributions, probability is represented as a function called the probability density function, or density function. These functions must be greater than zero, and must not have an area greater than 1 under their curves. The functions are called "density functions" because they will graph a smooth curve showing values that are most likely or "dense".
Look at the example below which shows a normal curve:

We can see very quickly that observations are most "dense" between 40 and 50. To find out the exact probability of a value being between 40 and 50, we must calculate the area of the region between 40 and 50. The same is true to find the probability of a value being less than 40. We must calculate the area under the curve that is less than 40. Thus we calculate the area under the curve for any probabilities we want to find.
Wednesday, February 25, 2009
Geometric Distribution
Suppose we wanted to know the chances of flipping a coin and only seeing a head by the fourth flip, how can we find this?
We can use the geometric distribution which calculates the probability of the number of failures before a success in a Bernouli trail.
The formula is
p(x) = (1-p)xp, where x = 0,1,2,...
Where p(x) is the number of failures, or for our example, the number of tails.
So to apply the formula, what are the chances of flipping a head for the first time on the 4th toss? (This means flipping 3 tails first)
p(x) = number of failures before flipping a head (3)
p(3) = (1 - 0.5)3(0.5) = 0.0625 or around 6%
Pretty low odds!
We can use the geometric distribution which calculates the probability of the number of failures before a success in a Bernouli trail.
The formula is
p(x) = (1-p)xp, where x = 0,1,2,...
Where p(x) is the number of failures, or for our example, the number of tails.
So to apply the formula, what are the chances of flipping a head for the first time on the 4th toss? (This means flipping 3 tails first)
p(x) = number of failures before flipping a head (3)
p(3) = (1 - 0.5)3(0.5) = 0.0625 or around 6%
Pretty low odds!
Monday, February 23, 2009
Binomial Distribution
The binomial distribution is used for multiple Bernouli Trials.
Its formula is written as follows:
p(x) = (n choose x) px * (1-p)n-x , x=0,1,2,....,n
The n choose x part is combinatorial.
n choose x = n! / x!(n-x)! where n is the number of outcomes, and x is the number of outcomes desired.
Example:
Suppose you take a true or false test with 10 questions, what are the chances you get 7 questions right if you just take random guesses? This is a true false so p=50% or .5
p(x) = (10 choose 7) (.5)7*(.5)3
= 10! / 7!*3! *.0078 * 0.125 = 30 * .0078 * 0.125 = 0.029
So you would only have about a 3% chance! Quite amazing. Of course, this means you would have a 97% chance of getting at least 3 wrong, which is not so amazing when you think about it.
Its formula is written as follows:
p(x) = (n choose x) px * (1-p)n-x , x=0,1,2,....,n
The n choose x part is combinatorial.
n choose x = n! / x!(n-x)! where n is the number of outcomes, and x is the number of outcomes desired.
Example:
Suppose you take a true or false test with 10 questions, what are the chances you get 7 questions right if you just take random guesses? This is a true false so p=50% or .5
p(x) = (10 choose 7) (.5)7*(.5)3
= 10! / 7!*3! *.0078 * 0.125 = 30 * .0078 * 0.125 = 0.029
So you would only have about a 3% chance! Quite amazing. Of course, this means you would have a 97% chance of getting at least 3 wrong, which is not so amazing when you think about it.
Bernoulli Trial
A Bernoulli trial is any experiment in which there can be only two outcomes, usually thought of as a success or failure.
Examples of this can be a coin flip, whether or not you pass a test, or the chances of catching the bus to school.
Assign a 1 to the chance of the event happening, and a 0 to it not happening.
Because discrete distributions have probabilities between 0 and 1, and cannot sum to more than one, a success is defined as p and a failure as 1-p
So the distribution of a Bernoulli trial is seen as
p(x)
0 = 1-p
1 = p
Examples of this can be a coin flip, whether or not you pass a test, or the chances of catching the bus to school.
Assign a 1 to the chance of the event happening, and a 0 to it not happening.
Because discrete distributions have probabilities between 0 and 1, and cannot sum to more than one, a success is defined as p and a failure as 1-p
So the distribution of a Bernoulli trial is seen as
p(x)
0 = 1-p
1 = p
Sunday, February 22, 2009
Discrete Random Variables
It should be known that discrete numbers in mathematics and statistics are not ones that know how to sneak around. Instead, they are countable numbers, even countably infinite numbers. If numbers are not discrete then they are said to be continuous, or uncountable.
In the situation of a coin flip, we can assign a 1 to the outcome of a head, and a 0 to the outcome of a tail. Thus we have transformed the outcome of a coin flip to a discrete random variable, or something that is countable and random.
Discrete distributions must always have probabilities between 0 and 1 and all probabilities must sum to 1.
In math this is
0 < = p(x) < = 1
and Sum(p(x)) = 1
In the situation of a coin flip, we can assign a 1 to the outcome of a head, and a 0 to the outcome of a tail. Thus we have transformed the outcome of a coin flip to a discrete random variable, or something that is countable and random.
Discrete distributions must always have probabilities between 0 and 1 and all probabilities must sum to 1.
In math this is
0 < = p(x) < = 1
and Sum(p(x)) = 1
Saturday, February 21, 2009
Bayes Theorem
Bayes theorem is an extension of the theorem of total probability.
Again, we are in a situation where all events in a sample space are mutually exclusive and exhaustive, but this time we want to find conditional probability as opposed to just probability.
We can do this with Bayes theorem which states that the conditional probability of any event (Ei) is
P(Ei,F) = (P(F,Ei)*P(Ei))/(The theorem of total probability)
Recall the theorem of total probability is:
P(F) = P(F and E1) + (F and E2) + (F and E3) + ...(as many as it takes to get "total" probability. "and" in the formula can me taken to mean multiplication or times.)
So in other words we are taking the product of the conditional probability of the outcome, with the probability of the outcome and dividing it by the total probability.
Consider the same example with the factories:
Let us say a company buys parts from 3 other companies.
It gets
60% from company A
40% from company B
20% from company C
Company A ships defective parts 1% of the time (0.01)
Company B ships defective parts 5% of the time (0.05)
Company C ships defective parts 10% of the time (0.10)
Bayes theorem can help us answer the question, what are the chances that a defective part in our company came from company A?
Here the conditional probability of the outcome (defective if from A) is 0.01
The chance of the outcome (bought from A) is 0.60
The probability of any part that is being bought can be found using the total probability theorem. We did that yesterday and found the probability to be 0.046(4.6%)
Bayes theorem says the chances the defective part is from company A is
(0.01*0.60) / 0.046 = 0.13 or 13%
Surprisingly higher than the chance of getting any defective product, but it is because such a large portion of purchases are from that company.
Again, we are in a situation where all events in a sample space are mutually exclusive and exhaustive, but this time we want to find conditional probability as opposed to just probability.
We can do this with Bayes theorem which states that the conditional probability of any event (Ei) is
P(Ei,F) = (P(F,Ei)*P(Ei))/(The theorem of total probability)
Recall the theorem of total probability is:
P(F) = P(F and E1) + (F and E2) + (F and E3) + ...(as many as it takes to get "total" probability. "and" in the formula can me taken to mean multiplication or times.)
So in other words we are taking the product of the conditional probability of the outcome, with the probability of the outcome and dividing it by the total probability.
Consider the same example with the factories:
Let us say a company buys parts from 3 other companies.
It gets
60% from company A
40% from company B
20% from company C
Company A ships defective parts 1% of the time (0.01)
Company B ships defective parts 5% of the time (0.05)
Company C ships defective parts 10% of the time (0.10)
Bayes theorem can help us answer the question, what are the chances that a defective part in our company came from company A?
Here the conditional probability of the outcome (defective if from A) is 0.01
The chance of the outcome (bought from A) is 0.60
The probability of any part that is being bought can be found using the total probability theorem. We did that yesterday and found the probability to be 0.046(4.6%)
Bayes theorem says the chances the defective part is from company A is
(0.01*0.60) / 0.046 = 0.13 or 13%
Surprisingly higher than the chance of getting any defective product, but it is because such a large portion of purchases are from that company.
Friday, February 20, 2009
Theorem of Total Probability
Suppose we are in a situation where all events in a sample space are mutually exclusive and exhaustive.
Mutually exclusive means the outcomes are separate from each other, like each time you roll a die.
Exhaustive means all outcomes are accounted for. (You will see in the example)
Example.
Let us say a company buys parts from 3 other companies.
It gets
60% from company A
40% from company B
20% from company C
Company A ships defective parts 1% of the time (0.01)
Company B ships defective parts 5% of the time (0.05)
Company C ships defective parts 10% of the time (0.10)
What are the odds of the company buying a defective part?
Now we have a situation that is exhaustive since all 3 companies comprise 100% of the outcomes. It is also mutually exclusive since one company doesn't affect the other and is "separate".
The theorem of total probability states that when we have an event that is mutually exclusive and exhaustive it can be found by adding the combination of disjoint outcomes. That is to say looking at each company separately and adding them together.
The way to write this is
P(defective part is bought) = P(defective shipped from A) + P(defective shipped from B) + P(defective shipped from C). This represents a "total" account of all outcomes.
The math formula looks like
P(F) = P(F and E1) + (F and E2) + (F and E3) + ...(as many as it takes to get "total" probability. "and" in the formula can me taken to mean multiplication or times.)
The P(defective from a company) is the portion bought from any company times(x) the chance the chance sends something defective.
P(A defective) = 0.6*0.01 = 0.006
P(B defective) = 0.4*0.05 = 0.02
P(C defective) = 0.2*0.10 = 0.02
So
P(defective part is bought) = 0.006 + 0.02 + 0.02 = 0.046 = 4.6%
Mutually exclusive means the outcomes are separate from each other, like each time you roll a die.
Exhaustive means all outcomes are accounted for. (You will see in the example)
Example.
Let us say a company buys parts from 3 other companies.
It gets
60% from company A
40% from company B
20% from company C
Company A ships defective parts 1% of the time (0.01)
Company B ships defective parts 5% of the time (0.05)
Company C ships defective parts 10% of the time (0.10)
What are the odds of the company buying a defective part?
Now we have a situation that is exhaustive since all 3 companies comprise 100% of the outcomes. It is also mutually exclusive since one company doesn't affect the other and is "separate".
The theorem of total probability states that when we have an event that is mutually exclusive and exhaustive it can be found by adding the combination of disjoint outcomes. That is to say looking at each company separately and adding them together.
The way to write this is
P(defective part is bought) = P(defective shipped from A) + P(defective shipped from B) + P(defective shipped from C). This represents a "total" account of all outcomes.
The math formula looks like
P(F) = P(F and E1) + (F and E2) + (F and E3) + ...(as many as it takes to get "total" probability. "and" in the formula can me taken to mean multiplication or times.)
The P(defective from a company) is the portion bought from any company times(x) the chance the chance sends something defective.
P(A defective) = 0.6*0.01 = 0.006
P(B defective) = 0.4*0.05 = 0.02
P(C defective) = 0.2*0.10 = 0.02
So
P(defective part is bought) = 0.006 + 0.02 + 0.02 = 0.046 = 4.6%
Thursday, February 19, 2009
Conditional Probability
Conditional probability is used to calculate probability when we have information that can make an event more likely.
For example:
What are the chances of guessing the number rolled on an even 6 sided die?
Since the sample space is {1,2,3,4,5,6} the chances are 1/6
But suppose the person rolling it gave you a hint and told you the number was odd, now what are your chances?
The sample space of odd numbers is {1,3,5} so your chances are 1/3
This is evident in such a small sample space, but we can use a formula for larger sample spaces.
P(E|F) = P(E and F)/P(F)
P(E|F) is read as probability of E given F. In this case E is the chance of guessing the number and F is the chance of the number being odd.
The probability of getting a number that is odd is 1/2 since half the numbers on a six sided die are odd. So P(F)=1/2
The probability of the number being odd and of you guessing the number is still (1/6)
so P(E and F) is 1/6
using the formula, the conditional probability P(E|F) that you can guess the number (E) given that you know it is odd(F) is
P(E|F) = (1/6) / (1/2) = (1/3)
So the formula gives us the same answer we previously saw.
For example:
What are the chances of guessing the number rolled on an even 6 sided die?
Since the sample space is {1,2,3,4,5,6} the chances are 1/6
But suppose the person rolling it gave you a hint and told you the number was odd, now what are your chances?
The sample space of odd numbers is {1,3,5} so your chances are 1/3
This is evident in such a small sample space, but we can use a formula for larger sample spaces.
P(E|F) = P(E and F)/P(F)
P(E|F) is read as probability of E given F. In this case E is the chance of guessing the number and F is the chance of the number being odd.
The probability of getting a number that is odd is 1/2 since half the numbers on a six sided die are odd. So P(F)=1/2
The probability of the number being odd and of you guessing the number is still (1/6)
so P(E and F) is 1/6
using the formula, the conditional probability P(E|F) that you can guess the number (E) given that you know it is odd(F) is
P(E|F) = (1/6) / (1/2) = (1/3)
So the formula gives us the same answer we previously saw.
Labels:
conditional probability,
probability,
statistics
Wednesday, February 18, 2009
P(G or C) = P(G) + P(C) - P(G and C)
P(G or C) = P(G) + P(C) - P(G and C)
When we look for the probability of one event or the other happening we need to add the chance of the first happening with the chance of the second happening, then we need to subtract the probability of both of them happening in order not to over-estimate the chances.
Example:
We are in a store where detailed tracking can tell us the chances of...
a person buying gum P(G) is 0.4
a person buying chocolate P(C) is 0.7
and a person buying both P(G and C) is 0.2
What is the probability that a person buys gum or chocolate?
P(G or C) = P(G) + P(C) - P(G and C)
P(G or C) = 0.4 + 0.7 - 0.2 = 0.9
There is a 90% chance of a customer buying either of those products.
------------------------------
The chances that a customer does not buy gum or chocolate is the complement.
P(not G and not C) = 1 - P(G or C)
or 1 - 0.9 = 0.1 so there is a 10% chance the customer will not buy either...
When we look for the probability of one event or the other happening we need to add the chance of the first happening with the chance of the second happening, then we need to subtract the probability of both of them happening in order not to over-estimate the chances.
Example:
We are in a store where detailed tracking can tell us the chances of...
a person buying gum P(G) is 0.4
a person buying chocolate P(C) is 0.7
and a person buying both P(G and C) is 0.2
What is the probability that a person buys gum or chocolate?
P(G or C) = P(G) + P(C) - P(G and C)
P(G or C) = 0.4 + 0.7 - 0.2 = 0.9
There is a 90% chance of a customer buying either of those products.
------------------------------
The chances that a customer does not buy gum or chocolate is the complement.
P(not G and not C) = 1 - P(G or C)
or 1 - 0.9 = 0.1 so there is a 10% chance the customer will not buy either...
Tuesday, February 17, 2009
P(E) + P(not E) = 1
P(E) + P(not E) = 1
This is because the probability of any event in the sample space must equal 1. Therefore if we know the probability of E we can also find the probability of not E.
Thus if we want to know the probability of not rolling a 2 on an even die we can say
P(rolling a 2) = 1/6
1/6 + P(not rolling a 2) = 1
P(not rolling a 2) = 1 - (1/6) = (5/6)
This is because the probability of any event in the sample space must equal 1. Therefore if we know the probability of E we can also find the probability of not E.
Thus if we want to know the probability of not rolling a 2 on an even die we can say
P(rolling a 2) = 1/6
1/6 + P(not rolling a 2) = 1
P(not rolling a 2) = 1 - (1/6) = (5/6)
Monday, February 16, 2009
Every probability must be greater than or equal to 0 and less than or equal to 1
Every probability must be greater than or equal to 0 and less than or equal to 1
That is to say
0 < = p < = 1
This is because the denominator of any probability is the entire sample space of any outcome.
No outcome, or the null event, would lead to a probability of 0.
That is to say
0 < = p < = 1
This is because the denominator of any probability is the entire sample space of any outcome.
No outcome, or the null event, would lead to a probability of 0.
Sunday, February 15, 2009
Defining and Calculating Probability
Yesterday we looked at sample spaces, outcomes, and events. Today we will look at ways to determine probability.
Again, consider the die. Imagine we wanted to know the probability of rolling an odd number. The sample space for a die is [1,2,3,4,5,6] and the outcomes of rolling an odd number are [1,3,5] so to calculate this probability we take the number of odd outcomes and divide it by the total number of outcomes.
In this case it is 3/6 or 1/2 or 50%. This is only true if the die is not slanted, that is to say, all outcomes are equally likely.
The second way of calculating probability can be used to test if the die is honest. This is found by rolling the die many times, around 100 and seeing how many times an odd number comes up. So in this case we calculate the probability by counting the number of times an odd number occurs over the number of times we roll the die.
Suppose we do this 100 times and find we rolled 55 odd numbers. Then we see that 55/100 times we rolled an odd, or 55% of the time. This is close enough to 50% to say that the die is honest. After rolling the die 1000 times or even 10,000 times we would expect the number to get closer and closer to 50%.
This second method of probability can also be used in times we we do not know the sample space. Let us say we want to know the probability of making a sale when a customer walks into our shop. There is no way to calculate this theoretically(the first method) and we must do it by counting. Assume that 100 people walk into the shop, and only 20 people end up making a purchase, then we conclude that the probability of making a sale is 20/100 or 20%.
Again, consider the die. Imagine we wanted to know the probability of rolling an odd number. The sample space for a die is [1,2,3,4,5,6] and the outcomes of rolling an odd number are [1,3,5] so to calculate this probability we take the number of odd outcomes and divide it by the total number of outcomes.
In this case it is 3/6 or 1/2 or 50%. This is only true if the die is not slanted, that is to say, all outcomes are equally likely.
The second way of calculating probability can be used to test if the die is honest. This is found by rolling the die many times, around 100 and seeing how many times an odd number comes up. So in this case we calculate the probability by counting the number of times an odd number occurs over the number of times we roll the die.
Suppose we do this 100 times and find we rolled 55 odd numbers. Then we see that 55/100 times we rolled an odd, or 55% of the time. This is close enough to 50% to say that the die is honest. After rolling the die 1000 times or even 10,000 times we would expect the number to get closer and closer to 50%.
This second method of probability can also be used in times we we do not know the sample space. Let us say we want to know the probability of making a sale when a customer walks into our shop. There is no way to calculate this theoretically(the first method) and we must do it by counting. Assume that 100 people walk into the shop, and only 20 people end up making a purchase, then we conclude that the probability of making a sale is 20/100 or 20%.
Saturday, February 14, 2009
Probability: Events, Outcomes, and Sample Spaces
Probability is one of the least intuitive aspects of statistics. If it wasn't, Casinos wouldn't net the billions of dollars they do each year.
What do we need to know to get a grounding in probability?
The first thing is the sample space, this is the set of all possible outcomes. For a coin it is heads or tails, for a die it is [1,2,3,4,5,6] and for the height of a person it is [x:x>0]
Outcomes are the result of any random event that we want to predict, i.e. we roll a die and a 2 comes up.
An Event is a desired outcome and is often denoted with a capital letter. For the dice we can define the event, A, as A=2.
Imagine we roll the die again and a 5 is the outcome. Then our desired event did not happen.
What do we need to know to get a grounding in probability?
The first thing is the sample space, this is the set of all possible outcomes. For a coin it is heads or tails, for a die it is [1,2,3,4,5,6] and for the height of a person it is [x:x>0]
Outcomes are the result of any random event that we want to predict, i.e. we roll a die and a 2 comes up.
An Event is a desired outcome and is often denoted with a capital letter. For the dice we can define the event, A, as A=2.
Imagine we roll the die again and a 5 is the outcome. Then our desired event did not happen.
Labels:
events,
outcomes,
probability,
sample spaces,
statistics
Bivariate Data
Bivariate data is a fancy way of saying "data with two variables".
Variables can be anything:
number of apples and number of oranges
number of church goers and number of bibles
number of ciggies smoked and number of people with cancer
number of guns and amount of ammo
number of plastic toys sold and number of cartoons
From this list we can see that bivariate data is suggestive. Did you hear yourself say: "Yeah, totally related, that definitely causes the other".
And so comes one of the most notorious dilemmas in statistics: Causation vs. Correlation.
Causation means that one causes the other, like the more you drive your car, the less gas you have in the tank.
Correlation is mere chance, but not related. For example, if we were to look at the number of people paying taxes and the number of people who die we would find a pretty good correlation, but, this doesn't count since taxes don't kill you...no matter how convinced you are that they do.
Consider this example:
Here we see that the more donuts a person eats per day, the higher their weight. Does that really mean that eating more donuts will mean you weigh more? What about other factors like exercise? To get a better appreciation of what is happening, it might be best to include exercise and create a multivariate model, but we will cover that later.
Variables can be anything:
number of apples and number of oranges
number of church goers and number of bibles
number of ciggies smoked and number of people with cancer
number of guns and amount of ammo
number of plastic toys sold and number of cartoons
From this list we can see that bivariate data is suggestive. Did you hear yourself say: "Yeah, totally related, that definitely causes the other".
And so comes one of the most notorious dilemmas in statistics: Causation vs. Correlation.
Causation means that one causes the other, like the more you drive your car, the less gas you have in the tank.
Correlation is mere chance, but not related. For example, if we were to look at the number of people paying taxes and the number of people who die we would find a pretty good correlation, but, this doesn't count since taxes don't kill you...no matter how convinced you are that they do.
Consider this example:

Here we see that the more donuts a person eats per day, the higher their weight. Does that really mean that eating more donuts will mean you weigh more? What about other factors like exercise? To get a better appreciation of what is happening, it might be best to include exercise and create a multivariate model, but we will cover that later.
Thursday, February 12, 2009
Measuring dispersion in Sample Data
Various tools can be used in measuring dispersion in sample data, because it is unlikely that any sample will contain the absolute lowest and highest value on the population it can tend to underestimate actual dispersion.
The formula to calculate sample variance is similar to variance and is written as:
s2 = 1/(n-1) * sum(X(values)-mean))2
The only difference is that we divide by n-1 instead of n, because sample variance tends to be an underestimate.
Other tools to measure sample variance are quartiles or percentiles.
The median can be thought as the 50th percentile, since 50 of the values fall both above and below it. Thus with the 75th percentile, 75% of the values fall below it and 25% are above it, and so on. These simple percentiles can give a good estimate of dispersion in the sample.
The formula to calculate sample variance is similar to variance and is written as:
s2 = 1/(n-1) * sum(X(values)-mean))2
The only difference is that we divide by n-1 instead of n, because sample variance tends to be an underestimate.
Other tools to measure sample variance are quartiles or percentiles.
The median can be thought as the 50th percentile, since 50 of the values fall both above and below it. Thus with the 75th percentile, 75% of the values fall below it and 25% are above it, and so on. These simple percentiles can give a good estimate of dispersion in the sample.
Wednesday, February 11, 2009
Variance and Standard Error
In addition to dispersion we can also measure distribution of data with variance and standard error.
The variance is found by subtracting each observation from the mean, squaring it, then summing them all together. Mathematically this is:
Variance = Sum(n-u)^2/N
were n is any observation, and u is the mean.
The Standard deviation is simply the square root of this number.
The variance is found by subtracting each observation from the mean, squaring it, then summing them all together. Mathematically this is:
Variance = Sum(n-u)^2/N
were n is any observation, and u is the mean.
The Standard deviation is simply the square root of this number.
Tuesday, February 10, 2009
Measuring dispersion
Yesterday we talked about measuring central tendency. This is a good statistic, but it is even better when it is partnered with its side kick: dispersion.
Consider the diagram:
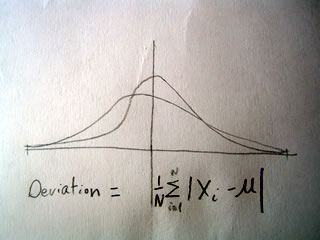
As we can see, the two distributions of data have similar central tendencies, but different amounts of dispersion.
One way to measure dispersion is to take the average of each value in the data set subtracted from the mean, using the formula shown in the picture.
Notice the symbol for summation of the absolute value of all observations subtracted from the mean.
Consider the diagram:

As we can see, the two distributions of data have similar central tendencies, but different amounts of dispersion.
One way to measure dispersion is to take the average of each value in the data set subtracted from the mean, using the formula shown in the picture.
Notice the symbol for summation of the absolute value of all observations subtracted from the mean.
Monday, February 9, 2009
Measures of Central Tendency in Numerical Data
Measuring central tendency in a distribution of data(numbers) provides a one-digit statistic, or descriptive source of information, that convey a lot of information about that data.
It is not as complicated as it sounds, consider the three most common ways of measuring central tendency: mean(average),median, and mode.
Consider a set of numerical data {1,3,4,5,5,6,6,7,8,10) N=10
Capital N is commonly used to represent the total number in the set(population) of data(the sample).
The mean, or average, is found by adding all elements of the data and then dividing by the total number in the set.
Thus
mean = 1+3+4+5+5+6+6+7+8+10/10 = 55/10 = 5.5
So the mean or average is 5.5
The median is found by ordering the numbers from lowest to highest and locating the value in the middle.
In this case, both 5 and 6 are in the middle, thus the median is the average of the two or 5+6/2 = 5.5
The mode is the most frequent value in the data set. For our example set it both 5 and 6 appear twice, and thus, they are both the mode.
It is no accident that the mean, median, and mode produce numbers which are either equal or close. Measures of central tendency are similar, after all the number which appears most (mode) is expected to most affect the average.
It is not as complicated as it sounds, consider the three most common ways of measuring central tendency: mean(average),median, and mode.
Consider a set of numerical data {1,3,4,5,5,6,6,7,8,10) N=10
Capital N is commonly used to represent the total number in the set(population) of data(the sample).
The mean, or average, is found by adding all elements of the data and then dividing by the total number in the set.
Thus
mean = 1+3+4+5+5+6+6+7+8+10/10 = 55/10 = 5.5
So the mean or average is 5.5
The median is found by ordering the numbers from lowest to highest and locating the value in the middle.
In this case, both 5 and 6 are in the middle, thus the median is the average of the two or 5+6/2 = 5.5
The mode is the most frequent value in the data set. For our example set it both 5 and 6 appear twice, and thus, they are both the mode.
It is no accident that the mean, median, and mode produce numbers which are either equal or close. Measures of central tendency are similar, after all the number which appears most (mode) is expected to most affect the average.
Labels:
average,
central tendency,
mean,
median,
mode,
statistics
Sunday, February 8, 2009
Frequency and Relative frequency, (Counts and percentages)
Frequencies are probably the most popular statistics.
A frequency is nothing more than a count.
And a relative frequency is a percentage.
Thus if we have a sample of 10 marbles we may count
4 red marbles
3 green marbles
2 blue marbles
1 yellow marble
The 4,3,2,1 are their counts or frequencies and their relative frequency would be the percentage they represent of the sample of 10.
We find a percentage dividing the count by the sample size, like
4/10 = 0.4 or 40%
4/10 = 0.2 or 30%
4/10 = 0.3 or 20%
4/10 = 0.1 or 10%
Data like this is often seen in the form of a bar chart, or a pie chart and is one of the most popular ways to present data for drawing conclusions.
A frequency is nothing more than a count.
And a relative frequency is a percentage.
Thus if we have a sample of 10 marbles we may count
4 red marbles
3 green marbles
2 blue marbles
1 yellow marble
The 4,3,2,1 are their counts or frequencies and their relative frequency would be the percentage they represent of the sample of 10.
We find a percentage dividing the count by the sample size, like
4/10 = 0.4 or 40%
4/10 = 0.2 or 30%
4/10 = 0.3 or 20%
4/10 = 0.1 or 10%
Data like this is often seen in the form of a bar chart, or a pie chart and is one of the most popular ways to present data for drawing conclusions.
Saturday, February 7, 2009
Statistics, Basic Concept and Key Terms
The next series of days will focus on Statistics.
Statistics is the science and art of collecting, analyzing, and making conclusions about data. All data is collected from a set population. Subsets of the population can be called members, or units. If every subset of the population is collected, then we have a census, however, often just a small portion of the population is sampled. The sample is then thought to represent the whole population.
Care must be taken when choosing any given sample. For example, if we want to get an idea of how a population will vote on a new cigarette tax it does no good to sample non-voters like children. Also, the sample must be random in order to assure accurate results. If we only ask voters leaving a cigarette store, we are not likely to get good results and arrive to correct conclusions.
Statistics is the science and art of collecting, analyzing, and making conclusions about data. All data is collected from a set population. Subsets of the population can be called members, or units. If every subset of the population is collected, then we have a census, however, often just a small portion of the population is sampled. The sample is then thought to represent the whole population.
Care must be taken when choosing any given sample. For example, if we want to get an idea of how a population will vote on a new cigarette tax it does no good to sample non-voters like children. Also, the sample must be random in order to assure accurate results. If we only ask voters leaving a cigarette store, we are not likely to get good results and arrive to correct conclusions.
Friday, February 6, 2009
Proof of Herons Formula to find the area of a non-right triangle
Proof of Herons Formula to find the area of a non-right triangle
Consider the following triangle:
There are no right angles in the triangle, so therefore we must use Heron's forumla which first defines a variable s
s=1/2(a+b+c) where a,b,c each represent the length of a side.
then the area of the triangle is equal to
sqrt(s(s-a)(s-b)(s-c))
For the example we see that s=21
and the area is equal to
sqrt(21(21-10)(21-15)(21-17))
=
sqrt(21*11*6*4)=sqrt(5,544)=~74.46 which is the area of the triangle.
How do we prove Herons formula? Consider the triangle:
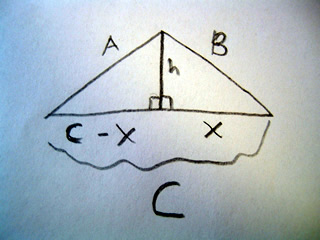
Here we have taken a triangle with no right angles, and cut a line so that we create two right triangles, and two new lengths at the base: x, and C-x. Now we need to solve for two unknown values x and h. We will solve for x first.
We can use pythagorean theorem to create equations for our new values, we see we have:
x2 + h2 = B2
and
(c-x)2 + h2 = A2
=
C2 - 2cx + x2+ h2 = A2
We know that B= x2+h2 so we substitute that in to the equation above and get
C2 - 2cx + B2 = A2
Now we can solve for x!
x= (A2 - B2 - C2) / - 2c
Now we have x we can plug it back in to the equation
x2 + h2 = B2
thus
h = sqrt(B2 - (A2 - B2 - C2) / - 2c)2)
Now, we know our base is equal to C and our height is equal to h, if we substitute these two values into the formula for the area of a triangle we get
(1/2)*b*h = 1/2*C2*sqrt(B2 - (A2 - B2 - C2) / - 2c)2)
That is a complicated formula, so Heron found that you could define a term
s = (1/2)*( A + B + C) and then found the area formula could become a simpler
sqrt(s(s-a)(s-b)(s-c))
If you plug s in to the area formula above you will find the result we saw above:
1/2*C2*sqrt(B2 - (A2 - B2 - C2) / - 2c)2)
which is the area of the triangle.
Consider the following triangle:
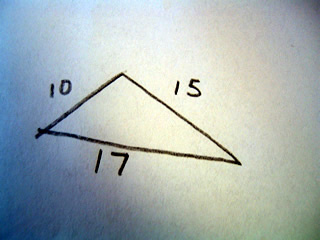
There are no right angles in the triangle, so therefore we must use Heron's forumla which first defines a variable s
s=1/2(a+b+c) where a,b,c each represent the length of a side.
then the area of the triangle is equal to
sqrt(s(s-a)(s-b)(s-c))
For the example we see that s=21
and the area is equal to
sqrt(21(21-10)(21-15)(21-17))
=
sqrt(21*11*6*4)=sqrt(5,544)=~74.46 which is the area of the triangle.
How do we prove Herons formula? Consider the triangle:

Here we have taken a triangle with no right angles, and cut a line so that we create two right triangles, and two new lengths at the base: x, and C-x. Now we need to solve for two unknown values x and h. We will solve for x first.
We can use pythagorean theorem to create equations for our new values, we see we have:
x2 + h2 = B2
and
(c-x)2 + h2 = A2
=
C2 - 2cx + x2+ h2 = A2
We know that B= x2+h2 so we substitute that in to the equation above and get
C2 - 2cx + B2 = A2
Now we can solve for x!
x= (A2 - B2 - C2) / - 2c
Now we have x we can plug it back in to the equation
x2 + h2 = B2
thus
h = sqrt(B2 - (A2 - B2 - C2) / - 2c)2)
Now, we know our base is equal to C and our height is equal to h, if we substitute these two values into the formula for the area of a triangle we get
(1/2)*b*h = 1/2*C2*sqrt(B2 - (A2 - B2 - C2) / - 2c)2)
That is a complicated formula, so Heron found that you could define a term
s = (1/2)*( A + B + C) and then found the area formula could become a simpler
sqrt(s(s-a)(s-b)(s-c))
If you plug s in to the area formula above you will find the result we saw above:
1/2*C2*sqrt(B2 - (A2 - B2 - C2) / - 2c)2)
which is the area of the triangle.
Thursday, February 5, 2009
Prove the area of a right triangle is equal to half the base*height
Prove that the area of a triangle is equal to 1/2*base*height.
The essence of this proof is to show that any right triangle can be made into a rectangle of the same base and height.
Consider the following two triangles:
Both these triangles can be made into rectangles with the same base and height as shown below:
The area of a rectangle is length times width, or in this case base times height.
The hypotenuse of the triangle cuts the rectangle directly in half, and thus the area of a triangle is 1/2 of a rectangle, or 1/2 base times height.
The essence of this proof is to show that any right triangle can be made into a rectangle of the same base and height.
Consider the following two triangles:
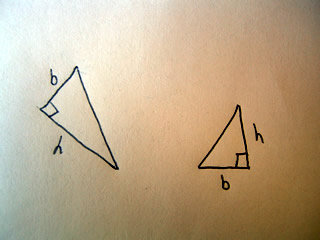
Both these triangles can be made into rectangles with the same base and height as shown below:

The area of a rectangle is length times width, or in this case base times height.
The hypotenuse of the triangle cuts the rectangle directly in half, and thus the area of a triangle is 1/2 of a rectangle, or 1/2 base times height.
Wednesday, February 4, 2009
The Law of Cosines
When we know the length of two sides of a triangle, and the angle between them, we can use the law of cosines to find the length of the remaining side.
The law of cosines states:
C^2 = A^2 + B^2 - 2AB*cos(theta)
Here is an example of the law of cosines:

Proof of the Law of Cosines
The law of cosines looks similar to the pythagorean theorem (C^2 = A^2 + B^2) and indeed the two are similar. What we have to do to prove the law of cosines is to create a right triangle and define coordinates for that right triangle so we can find our remaining side.
Consider the diagram below:

Imagine the triangle on a coordinate plane. We define the origin, the point (0,0) at the end of side B. Thus the coordinate to the left is (-B,0). The coordinate at the top of the triangle (A*cos(theta)-B,A*sin(theta)) is derived from the right triangle sketch in on the right of our triangle. Although the coordinates appear complex, keep in mind they represent two numbers:
(A*cos(theta)-B,A*sin(theta)) is equal to some (x,y) on the coordinate plane.
Now that we have defined some coordinates we can draw a line down from the top angle to some point on side B, this creates a right triangle as shown below.
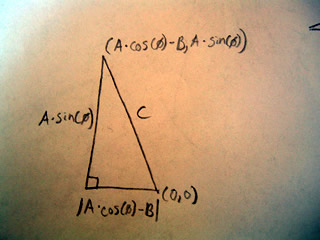
Using the coordinates which we defined we can define the length of the sides of this triangle.
The bottom side has length: |A*cos(theta)-B|.
A*cos(theta) comes from the dotted triangle we sketched in the previous image and represents the length that we have chopped off of side B. This the new length of the triangle is A*cos(theta)-B , it could also be B-A*cos(theta). Because we don't know which way to subtract, we take the absolute value so that both equations give us the same length, and write the distance as |A*cos(theta)-B|. The length of the vertical side also comes from the previous dotted triangle, and is simply A*sin(theta).
With these lengths now defined we can find C with the pythagorean theorem.
C2= (A*sin(theta)2 + (A*cos(theta) - B)2
Mutliply this out and you get
C2=A2*sin2(theta) +A2cos2(theta) - 2AB*cos(theta) + B2
Factoring out the A2 we get
C2=A2(sin2(theta)+cos2(theta))-2AB*cos(theta)+B2
Knowing that sin2(theta)+cos2(theta)=1 we get
C2=A2 - 2AB*cos(theta) + B2
whic is the Law of Cosines.
C2 = A2 + B2 - 2AB*cos(theta)
The law of cosines states:
C^2 = A^2 + B^2 - 2AB*cos(theta)
Here is an example of the law of cosines:

Proof of the Law of Cosines
The law of cosines looks similar to the pythagorean theorem (C^2 = A^2 + B^2) and indeed the two are similar. What we have to do to prove the law of cosines is to create a right triangle and define coordinates for that right triangle so we can find our remaining side.
Consider the diagram below:

Imagine the triangle on a coordinate plane. We define the origin, the point (0,0) at the end of side B. Thus the coordinate to the left is (-B,0). The coordinate at the top of the triangle (A*cos(theta)-B,A*sin(theta)) is derived from the right triangle sketch in on the right of our triangle. Although the coordinates appear complex, keep in mind they represent two numbers:
(A*cos(theta)-B,A*sin(theta)) is equal to some (x,y) on the coordinate plane.
Now that we have defined some coordinates we can draw a line down from the top angle to some point on side B, this creates a right triangle as shown below.
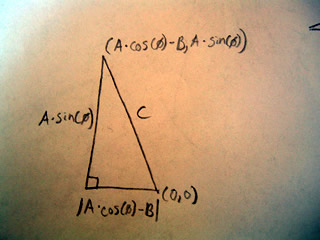
Using the coordinates which we defined we can define the length of the sides of this triangle.
The bottom side has length: |A*cos(theta)-B|.
A*cos(theta) comes from the dotted triangle we sketched in the previous image and represents the length that we have chopped off of side B. This the new length of the triangle is A*cos(theta)-B , it could also be B-A*cos(theta). Because we don't know which way to subtract, we take the absolute value so that both equations give us the same length, and write the distance as |A*cos(theta)-B|. The length of the vertical side also comes from the previous dotted triangle, and is simply A*sin(theta).
With these lengths now defined we can find C with the pythagorean theorem.
C2= (A*sin(theta)2 + (A*cos(theta) - B)2
Mutliply this out and you get
C2=A2*sin2(theta) +A2cos2(theta) - 2AB*cos(theta) + B2
Factoring out the A2 we get
C2=A2(sin2(theta)+cos2(theta))-2AB*cos(theta)+B2
Knowing that sin2(theta)+cos2(theta)=1 we get
C2=A2 - 2AB*cos(theta) + B2
whic is the Law of Cosines.
C2 = A2 + B2 - 2AB*cos(theta)
Tuesday, February 3, 2009
The Law of Sines
When we know the measure of the angles of a triangle, and the measure of one of its sides, we can use the law of sines to find the length of the other two sides.
The law sines states for any triangle with sides A,B, or C that
sin(a)/A = sin(b)/B = sin(c)/C
or equivalently
A/sin(a) = B/sin(b) = C/sin(c)
So if we have a triangle as such, with side x unknown we can find it by using the law of sines:
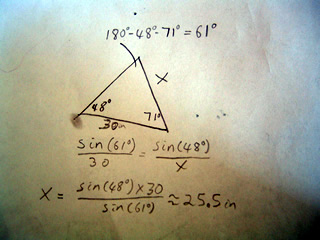
Proof of the Law of Sines
Consider the following diagram:
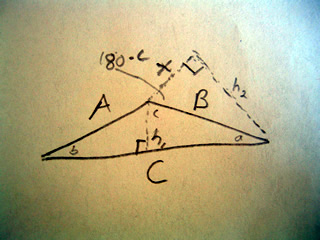
In the first step of the proof we divide the triangle into two right triangles by drawing a line of length h1.
Now we have two right triangles we can say that
sin(b)=h/A or h=A*sin(b)
similarly
sin(a)=h/B so h=B*sin(a)
now we can see that
B*sin(a)=h=A*sin(b)
divide both sides by AB and we get
sin(a)/A = sin(b)/B which is the first half of the law of sines.
For the next part, we draw a right triangle out from side B, creating a new length h2.
From this new triangle we see that
sin(b)=h/C and h=sin(b)*C
we also see that
sin(180-c) = h/B or h=sin(180-c)*B
but from the unit circle below we see that sin(180-c)=sin(c)
so we can write sin(c)*B=h and from this conclude
sin(b)*C=h=sin(c)*B
again we divide both sides by BC and get
sin(b)/B = sin(c)/C
so we have sin(a)/A=sin(b)/B=sin(c)/C which is the law of sines.
The law sines states for any triangle with sides A,B, or C that
sin(a)/A = sin(b)/B = sin(c)/C
or equivalently
A/sin(a) = B/sin(b) = C/sin(c)
So if we have a triangle as such, with side x unknown we can find it by using the law of sines:
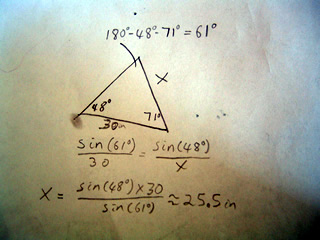
Proof of the Law of Sines
Consider the following diagram:

In the first step of the proof we divide the triangle into two right triangles by drawing a line of length h1.
Now we have two right triangles we can say that
sin(b)=h/A or h=A*sin(b)
similarly
sin(a)=h/B so h=B*sin(a)
now we can see that
B*sin(a)=h=A*sin(b)
divide both sides by AB and we get
sin(a)/A = sin(b)/B which is the first half of the law of sines.
For the next part, we draw a right triangle out from side B, creating a new length h2.
From this new triangle we see that
sin(b)=h/C and h=sin(b)*C
we also see that
sin(180-c) = h/B or h=sin(180-c)*B
but from the unit circle below we see that sin(180-c)=sin(c)

so we can write sin(c)*B=h and from this conclude
sin(b)*C=h=sin(c)*B
again we divide both sides by BC and get
sin(b)/B = sin(c)/C
so we have sin(a)/A=sin(b)/B=sin(c)/C which is the law of sines.
Labels:
law of sines,
right triangles,
sine,
trigonemtry,
trigonomentric proofs
Monday, February 2, 2009
An Example of Vector Physics
Assume you try to pull a box across the room. You exert 150 pounds of pressure (which you could measure with a spring) on the box, how much force will be used to drag the box and how much to lift it? This problem can be solved with trigonometry.

Thus from the sketch we see we can calculate horizontal force as
150 * cos(40) = 115 lbs of force
We get this equation knowing that the cosine of an angle is adjacent over hypotenuse, thus
adjacent = hypotenuse*cosine(angle)
or
115 = 150 * cos(40)
By the same method we can find the opposite side which will give us the force of lift.
150 * sin(40) = 96 pounds
Whether or not this is enough force to move the box depends on the friction and weight of the box, as well as several other variables.

Thus from the sketch we see we can calculate horizontal force as
150 * cos(40) = 115 lbs of force
We get this equation knowing that the cosine of an angle is adjacent over hypotenuse, thus
adjacent = hypotenuse*cosine(angle)
or
115 = 150 * cos(40)
By the same method we can find the opposite side which will give us the force of lift.
150 * sin(40) = 96 pounds
Whether or not this is enough force to move the box depends on the friction and weight of the box, as well as several other variables.
Sunday, February 1, 2009
Saturday, January 31, 2009
Trigonometric Arcfunctions
Arcfunctions, or inverse functions, of trigonometry allow you to find the degree of an angle if you have the ratios.
Thus arcsin(1/2) = 30 degrees
since sin(30) = 1/2
this can also be written as
sin-1(1/2) = 30 degrees
The arc functions can produce more than one value, for example
arcsin(sqrt2/2) can equal 90 degrees and 135 degrees.
As we learned when we covered functions in set theory, functions can be defined on any domain, and thus, the arc functions are defined to be between -90 and 90 degrees to avoid getting more than one output. That is -Pi/2 and Pi/2 radians.
Thus arcsin(1/2) = 30 degrees
since sin(30) = 1/2
this can also be written as
sin-1(1/2) = 30 degrees
The arc functions can produce more than one value, for example
arcsin(sqrt2/2) can equal 90 degrees and 135 degrees.
As we learned when we covered functions in set theory, functions can be defined on any domain, and thus, the arc functions are defined to be between -90 and 90 degrees to avoid getting more than one output. That is -Pi/2 and Pi/2 radians.
Labels:
domain,
functions,
set theory,
trigonometric functions
Friday, January 30, 2009
The Sine function And Circles
Yesterday we learned that sine is the y coordinate of any point on the unit circle. Thus if we take the circumference of the circle and place it on the x-axis from 0 to 2pi, we can evaluate sin at any point. The result is the graph that represent a stretched out circle.

Graph from wikipedia.
The curve of a circle occurs many places in nature and is used to model frequencies of energy, such as electricity and sound.

Graph from wikipedia.
The curve of a circle occurs many places in nature and is used to model frequencies of energy, such as electricity and sound.
Thursday, January 29, 2009
Prove that the coordinates of a particular angle on the unit circle are the cosine and sine of that angle.
Prove that the coordinates of a particular angle on the unit circle are the cosine and sine of that angle.
Consider the unit circle with coordinates x and y:
Cosine is defined as the side adjacent to the angle divided by the hypotenuse, (A/H), or in this case (x/1) so we see that cosine = x
Similarly sine is defined as the side opposite the angle divided by the hypotenuse, (O/H), or in this case (y/1) so we see that sine = 1
Thus we have proved that the coordinates of a particular angle on the unit circle are the cosine and sine of that angle, as shown below:

Consider the unit circle with coordinates x and y:

Cosine is defined as the side adjacent to the angle divided by the hypotenuse, (A/H), or in this case (x/1) so we see that cosine = x
Similarly sine is defined as the side opposite the angle divided by the hypotenuse, (O/H), or in this case (y/1) so we see that sine = 1
Thus we have proved that the coordinates of a particular angle on the unit circle are the cosine and sine of that angle, as shown below:

Wednesday, January 28, 2009
Finding coordinates on the Unit Circle
Coordinates can be found on the unit circle by inscribing 60, 45, and 30 degree triangles.
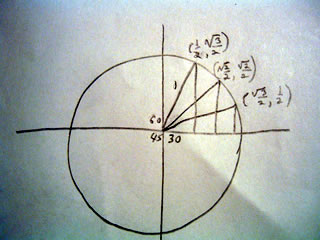
Thus triangles with
60 degrees corresponds to the coordinate (1/2,sqrt(3)/2)
45 degrees corresponds to the coordinate (sqrt(2)/2,sqrt(2)/2)
30 degrees corresponds to the coordinate (sqrt(3)/2,1/2)
So the adjacent side makes the x axis, the opposite side makes the y axis, and the hypotenuse always equals 1.

Thus triangles with
60 degrees corresponds to the coordinate (1/2,sqrt(3)/2)
45 degrees corresponds to the coordinate (sqrt(2)/2,sqrt(2)/2)
30 degrees corresponds to the coordinate (sqrt(3)/2,1/2)
So the adjacent side makes the x axis, the opposite side makes the y axis, and the hypotenuse always equals 1.
Labels:
coordinates,
trigonemtry,
unit circle coordinates
Tuesday, January 27, 2009
Unit Circle and Sample Angles
The unit circle is a circle with radius 1 and is used to evaluate trigonometric functions.
The unit circle can tell us the measure of any angle from the origin to an (x,y) coordinate, however, angles can be more than 360 degrees on the circle, as we see in the example.
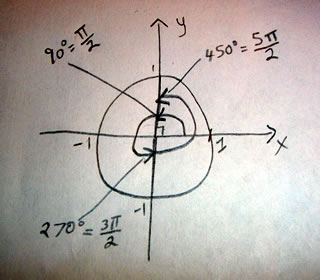
Thus at point (0,1) we have both
90 degrees or (Pi/2)
and
450 degrees or (5pi/2)
at point
(0,-1) we have 270 degrees or (3Pi/2)
Thus we see how the unit circle is used to measure angles, we will see in future posts how it relates to the trigonometric functions.
The unit circle can tell us the measure of any angle from the origin to an (x,y) coordinate, however, angles can be more than 360 degrees on the circle, as we see in the example.

Thus at point (0,1) we have both
90 degrees or (Pi/2)
and
450 degrees or (5pi/2)
at point
(0,-1) we have 270 degrees or (3Pi/2)
Thus we see how the unit circle is used to measure angles, we will see in future posts how it relates to the trigonometric functions.
Monday, January 26, 2009
Right Triangles in Equilateral Triangle
Equilateral triangles do not have right angles, making them difficult to work with in regards to trigonometric equations. This can be solved by cutting the triangle in half, thus creating two triangles.
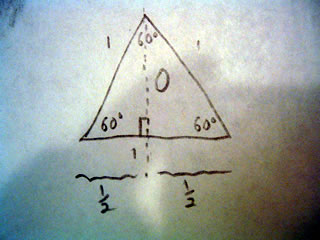
From the triangle above, we can find the length of the dotted line, 0, by pythagorean theorem.
This (1/2)2 + O2 = 12
=
(1/4) + O2 = 1
O = Sqrt(1-(1/4)) = sqrt(3/4) = sqrt(3)/2
The new angle at the top of the triangle can also be found, since all angles add up to 180, we get:
60 + y + 90 = 180
and so y=30 , exactly half of 60.
in degrees this is 30*(pi/180) = Pi/6

From the triangle above, we can find the length of the dotted line, 0, by pythagorean theorem.
This (1/2)2 + O2 = 12
=
(1/4) + O2 = 1
O = Sqrt(1-(1/4)) = sqrt(3/4) = sqrt(3)/2
The new angle at the top of the triangle can also be found, since all angles add up to 180, we get:
60 + y + 90 = 180
and so y=30 , exactly half of 60.
in degrees this is 30*(pi/180) = Pi/6
Sunday, January 25, 2009
Prove that an isosceles right traingle has 45, 45, and 90 degree angles
Prove that an isosceles right triangle has 45, 45, and 90 degree angles.
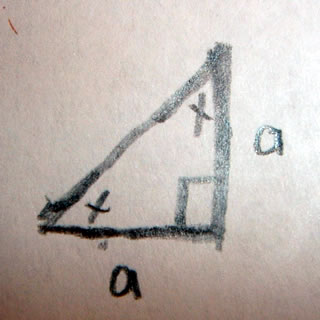
Remembering what we know about isosceles triangles we can find any two angles of a triangle if we know one angle.
Thus since we know one angle is equal to 90 degrees, the remaining two angles are equal to each other, and all the angles of a triangle must equal 180 degrees, we can say
2x + 90 = 180
solving we get x=45
Thus the angles are 45, 45, 90
or Pi/4 , Pi/4 , Pi/2 radians.
The Pythagorean theorem can be written as follows for isosceles right triangles
2a2 = Hypotenuse2
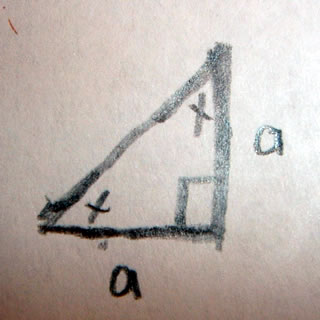
Remembering what we know about isosceles triangles we can find any two angles of a triangle if we know one angle.
Thus since we know one angle is equal to 90 degrees, the remaining two angles are equal to each other, and all the angles of a triangle must equal 180 degrees, we can say
2x + 90 = 180
solving we get x=45
Thus the angles are 45, 45, 90
or Pi/4 , Pi/4 , Pi/2 radians.
The Pythagorean theorem can be written as follows for isosceles right triangles
2a2 = Hypotenuse2
Saturday, January 24, 2009
Prove that tan2(x) + 1 = sec2(x)
Prove that tan2(x) + 1 = sec2(x)
We know that
sin2(x) + cos2(x) = 1
dividing both sides by cos2(x) we get
(sin2(x) + cos2(x))/cos2(x) = 1/cos2(x)
which equals
sin2(x)/cos2(x) + cos2(x)/cos2(x) = (1/cos(x))2
which can be re-written as
(sin(x)/(cos(x))2 + 1 = (1/cos(x))2
We know that tan2(x) = (sin(x)/(cos(x))2
and that (1/cos(x))2 = sec2(x)
So we can write
cot2(x) + 1 = sec2(x)
We know that
sin2(x) + cos2(x) = 1
dividing both sides by cos2(x) we get
(sin2(x) + cos2(x))/cos2(x) = 1/cos2(x)
which equals
sin2(x)/cos2(x) + cos2(x)/cos2(x) = (1/cos(x))2
which can be re-written as
(sin(x)/(cos(x))2 + 1 = (1/cos(x))2
We know that tan2(x) = (sin(x)/(cos(x))2
and that (1/cos(x))2 = sec2(x)
So we can write
cot2(x) + 1 = sec2(x)
Friday, January 23, 2009
Prove that sin^2(x) + cos^2(x) = 1
Prove that sin^2(x) + cos^2(x) = 1
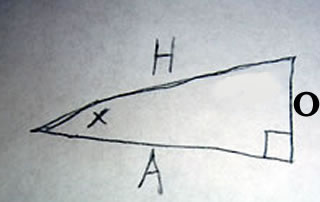
by Pythagorean Theorem A^2 + O^2 = H^2
Now, if we divide both sides by H^2 we get
(A^2 + O^2)/H^2 = H^2/H^2
which is
A^2/H^2 + O^2/H^2 = 1
which is
(A/H)^2 + (O/H)^2 = 1
now sin(x) = A/H and cos(x)=O/H so
sin^2(x) + cos^2(x) = 1

by Pythagorean Theorem A^2 + O^2 = H^2
Now, if we divide both sides by H^2 we get
(A^2 + O^2)/H^2 = H^2/H^2
which is
A^2/H^2 + O^2/H^2 = 1
which is
(A/H)^2 + (O/H)^2 = 1
now sin(x) = A/H and cos(x)=O/H so
sin^2(x) + cos^2(x) = 1
Thursday, January 22, 2009
Secant, cosecant, and cotangent.
After sine, cosine, and tangent, there are only 3 more possible ratios to be made from a triangle. These last relations are the inverse of the respective functions, they are secant (sec), cosecant (csc), and cotangent (cot).

x = The angle x
O = Opposite side of the angle x
A = Adjacent side of the angle x
H = Hypotenuse
sin(x) = O/H
csc(x) = H/O
cos(x) = A/H
sec(x) = H/A
tan(x) = O/A
cot(x) = A/O

x = The angle x
O = Opposite side of the angle x
A = Adjacent side of the angle x
H = Hypotenuse
sin(x) = O/H
csc(x) = H/O
cos(x) = A/H
sec(x) = H/A
tan(x) = O/A
cot(x) = A/O
Wednesday, January 21, 2009
Prove that tan(x) = sin(x)/cos(x)
Prove that tan(x) = sin(x)/cos(x)

sin(x) = (0/H)
cos(x) = (A/H)
Then sin(x)/cos(x) =
(O/H)/(A/H) =
(O/H)*(H/A) =
(O/A) = tan(x)
So sin(x)/cos(x) = tan(x)

sin(x) = (0/H)
cos(x) = (A/H)
Then sin(x)/cos(x) =
(O/H)/(A/H) =
(O/H)*(H/A) =
(O/A) = tan(x)
So sin(x)/cos(x) = tan(x)
Labels:
cool proofs,
cosine,
sine,
tangent,
trigonomentric proofs
Tuesday, January 20, 2009
Tangent
The tangent function is defined as the length of the side opposite the angle x divided by the length of the adjacent angle.
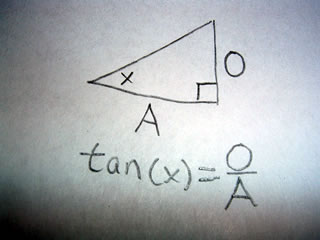
Thus if O=5 and A=3 then
tan(x)=5/3
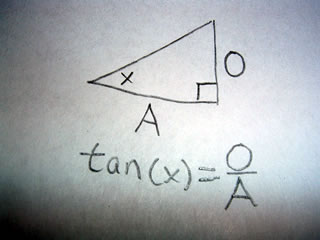
Thus if O=5 and A=3 then
tan(x)=5/3
Monday, January 19, 2009
A relationship between sine and cosine
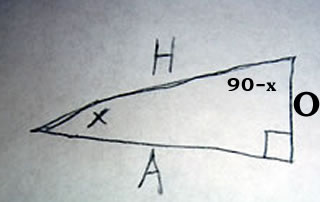
From the figure above the cosine of x can be defined as follows:
cos(x) = sin(90 - x)
This is because we know we have one 90 degree angle, a right angle, so the other two angles must equal 90 degrees, since the interior angles of a triangle always add up to 180 degrees. When the measure of two angles are dependent on each other in this way they can be called complements,. The name cosine originated this way, since it is the compliment of sine.
Sunday, January 18, 2009
Cosine
The cosine of an angle can be defined as the length of the adjacent side divided by the length of the hypotenuse.

This if A=4 and H=9 then
cos(x) = (4/9)

This if A=4 and H=9 then
cos(x) = (4/9)
Saturday, January 17, 2009
Sine: The first trigonometric function
The sine of an angle is defined as the length of the hypotenuse divided by the length of the opposite side.
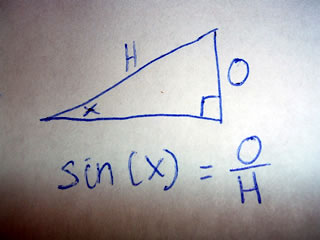
Thus if O=6 and H=10 then
sin(x) = 6/10
= 3/5
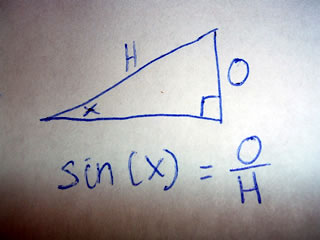
Thus if O=6 and H=10 then
sin(x) = 6/10
= 3/5
Friday, January 16, 2009
Pythagorean Triples
Pythagorean Triples occur when right angled triangles contain whole numbered sides. In other words, when a,b, and c are whole numbers for the diagram below.
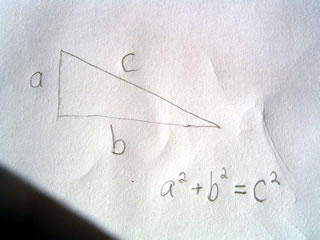
Thus if a=3 b=4 then c=5
We see 3^2 + 4^2 = 5^2 or 9 + 16 = 25
however, if b has a length of 5 (b=5) then we have
3^2 + 5^2 = 34 and the square root of 34 is 5.83095...
which isn't a whole number. Thus a right angled triangle with sides 3,4,5 is a Pythagorean triple, but a right angled triangle with sides 3,5,5.83095... isn't.
We can find Pythagorean triples (a,b,c) by taking any two whole number r and s, where r is greater than s (r > s)
then set
a= 2rs
b= r^2 - s^2
c= r^2 + s^2
As an example let r=5 and s=2
then
a=20
b=21
and
c=29
we see it is a Pythagorean triple because 20^2 + 21^2 = 29^2
or 400 + 441= 841
We can see how it works by plugging in the values for a and b.
Thus
a^2 + b^2 =
(2rs)^2 + (r^2 - s^2)^2 =
4(r^2)(s^2) + r^4 - 2(r^2)(s^2) + s^4 =
r^4 + 2(r^2)(s^2) + s^4 =
(r^2 + s^2)^2 = c^2
Thus
a^2 + b^2 = c^2
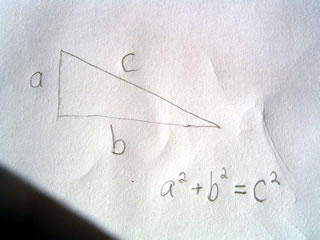
Thus if a=3 b=4 then c=5
We see 3^2 + 4^2 = 5^2 or 9 + 16 = 25
however, if b has a length of 5 (b=5) then we have
3^2 + 5^2 = 34 and the square root of 34 is 5.83095...
which isn't a whole number. Thus a right angled triangle with sides 3,4,5 is a Pythagorean triple, but a right angled triangle with sides 3,5,5.83095... isn't.
We can find Pythagorean triples (a,b,c) by taking any two whole number r and s, where r is greater than s (r > s)
then set
a= 2rs
b= r^2 - s^2
c= r^2 + s^2
As an example let r=5 and s=2
then
a=20
b=21
and
c=29
we see it is a Pythagorean triple because 20^2 + 21^2 = 29^2
or 400 + 441= 841
We can see how it works by plugging in the values for a and b.
Thus
a^2 + b^2 =
(2rs)^2 + (r^2 - s^2)^2 =
4(r^2)(s^2) + r^4 - 2(r^2)(s^2) + s^4 =
r^4 + 2(r^2)(s^2) + s^4 =
(r^2 + s^2)^2 = c^2
Thus
a^2 + b^2 = c^2
Thursday, January 15, 2009
The Pythagorean Theorem
The Pythagorean Theorem is probably the most well known theorem in trigonometry. It states that the sum of the squares of the sides of a right angle triangle is equal to the square of the hypotenuse.
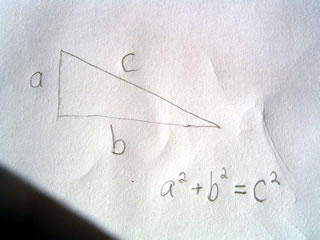
The proof of this theorem can be seen by making a square from four traingles. In the square it becomes evident that a^2 + b^2 = c^2

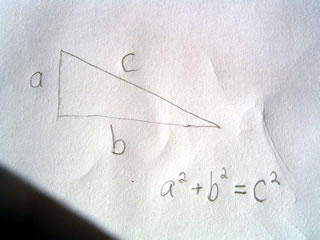
The proof of this theorem can be seen by making a square from four traingles. In the square it becomes evident that a^2 + b^2 = c^2

Wednesday, January 14, 2009
Scaling
Scaling of triangles occurs when one triangle is a copy of another triangle but has the length of its sized increased by some fixed factor x. In the example below we see two triangles. The second triangle is an enlarged version of the first triangle, and thus has been scaled up.
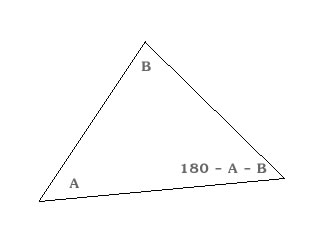
An interested property of scaled triangles is that the lengths of interior angles remains the same, no matter how large the triangle gets. You could have a triangle the size of the universe, and it would still have the same angle lengths.
Another interesting aspect is that if we know the length of any two similar sides we can calculate the scaling factor. Thus if the first triangle has a side with length 2 and the second a side with length 6, then we can say the scaling factor is 3. We can use this scaling factor to discern the lengths of the remaining sides of the larger triangle.


An interested property of scaled triangles is that the lengths of interior angles remains the same, no matter how large the triangle gets. You could have a triangle the size of the universe, and it would still have the same angle lengths.
Another interesting aspect is that if we know the length of any two similar sides we can calculate the scaling factor. Thus if the first triangle has a side with length 2 and the second a side with length 6, then we can say the scaling factor is 3. We can use this scaling factor to discern the lengths of the remaining sides of the larger triangle.
Tuesday, January 13, 2009
Isosceles and Equilateral Triangles
Isosceles triangles are triangles with two sides of equal length. Therefore if we know the measure of one angle we can calculate the measure of the remaining angles. If we know that the measure of the unequal angle is 30 degrees we can deduce that the remaining angles must each equal 75 degrees.
Let x equal the measure of our two equal angles. This 2x + 30 must equal 180, or the total measure of degrees in a triangle.
2x + 30 = 180
2x=150
x=75
Equilateral triangles are triangles which have sides of equal length and therefore angles of equal length. The angles of an equilateral triangle will always equal 60 degrees or (pi)/3 radians.
Let x equal the measure of our two equal angles. This 2x + 30 must equal 180, or the total measure of degrees in a triangle.
2x + 30 = 180
2x=150
x=75
Equilateral triangles are triangles which have sides of equal length and therefore angles of equal length. The angles of an equilateral triangle will always equal 60 degrees or (pi)/3 radians.
Monday, January 12, 2009
Prove that the interior angles of a triangle always add up to 180 degrees
Prove that the interior angles of a triangle always add up to 180 degrees.
In the drawing above the angles of the circles are equal and the angles of the squares are equal by properties of geometry.
Thus we can see that: circle + star + square = 180 degrees, or Pi Radians, since all 3 angles form a straight line.
We can use this fact to calculate the length of any angle in a triangle if we know the length of the other two angles.
Thus if
Angle 1 = 40 degrees
Angle 2 = 60 degrees
then angle 3 must equal 80 degrees to complete the sum of angles to 180 degrees.
similarly if
Angle 1 = Pi/4 radians
Angle 2 = Pi/4 radians
then Angle 3 must be equal to Pi/2 radians to complete the sum of angles to Pi.

In the drawing above the angles of the circles are equal and the angles of the squares are equal by properties of geometry.
Thus we can see that: circle + star + square = 180 degrees, or Pi Radians, since all 3 angles form a straight line.
We can use this fact to calculate the length of any angle in a triangle if we know the length of the other two angles.
Thus if
Angle 1 = 40 degrees
Angle 2 = 60 degrees
then angle 3 must equal 80 degrees to complete the sum of angles to 180 degrees.
similarly if
Angle 1 = Pi/4 radians
Angle 2 = Pi/4 radians
then Angle 3 must be equal to Pi/2 radians to complete the sum of angles to Pi.
Sunday, January 11, 2009
Converting Degrees to Radians and Radians to Degrees
Yesterday we learned about degrees and radians: two ways to measure an angle.
Today we will learn how to convert one measure to the other.
A full circle is equal to 360 degrees which is equal to 2(pi)
Thus 360 degrees = 2(pi) radians
dividing by 360 we get
1 degree = 2(pi)/360
or
1 degree = (pi)/180
conversely
1 radian = 180/(pi) degrees
Examples
How many radians equal 150 degrees?
To find this we multiply by pi/180 thus
150*(pi/180) = 5(pi)/6 radians
So 150 degrees equals 5(pi)/6 radians. Radians are typically written as fractions since pi is irrational. Irrational means it has an infinite number of decimals.
---------------
Now let us convert radians to degrees, how many degrees are in 7(pi)/12 radians?
To find this we multiply the radians by 180/pi and so we get
7(pi)/12 * 180/pi = 105 degrees
So there are 105 degrees in 7(pi)/12 radians.
Today we will learn how to convert one measure to the other.
A full circle is equal to 360 degrees which is equal to 2(pi)
Thus 360 degrees = 2(pi) radians
dividing by 360 we get
1 degree = 2(pi)/360
or
1 degree = (pi)/180
conversely
1 radian = 180/(pi) degrees
Examples
How many radians equal 150 degrees?
To find this we multiply by pi/180 thus
150*(pi/180) = 5(pi)/6 radians
So 150 degrees equals 5(pi)/6 radians. Radians are typically written as fractions since pi is irrational. Irrational means it has an infinite number of decimals.
---------------
Now let us convert radians to degrees, how many degrees are in 7(pi)/12 radians?
To find this we multiply the radians by 180/pi and so we get
7(pi)/12 * 180/pi = 105 degrees
So there are 105 degrees in 7(pi)/12 radians.
Saturday, January 10, 2009
Trigonometry: Degrees and Radians
I have decided to take up reviewing trigonometry as a goal for this blog. In the first look at trigonometry it is necessary to understand angles. Angles are create by the intersection of two lines. They can be measured in degrees or radians.
Degrees
There are 360 degrees in any possible angle, the widest angle forming a complete circle. The number 360 was chosen by the Babylonians who counted in groups of 60 (base 60) where as we count in groups of 10 (base 10). Thus 1/60th of a degree is called a minute and 1/60th of a minute is called a second. This terminology is still used by navigators today, but some also use decimals. In any case, two perpendicular lines, like in a capital L are said to have 90 degrees, a flat line ___ has 180 degrees and flipping the whole thing over completes the circle with 270 degrees and finally 360.
Radians
Radians are ways of measuring angles as they are drawing inside a circle. If we take the circumference of a circle we get C = 2(pi), thus we can draw a unit circle (circle with circumference = 1) around any angle and be able to express the measure of that angle in terms of radians. Thus the L would become (Pi/2) or 1/4 the circumference, which also equates to 90 degrees. The flat line ___ would become Pi, or half the circle, this would equate to 180 degrees.
Degrees
There are 360 degrees in any possible angle, the widest angle forming a complete circle. The number 360 was chosen by the Babylonians who counted in groups of 60 (base 60) where as we count in groups of 10 (base 10). Thus 1/60th of a degree is called a minute and 1/60th of a minute is called a second. This terminology is still used by navigators today, but some also use decimals. In any case, two perpendicular lines, like in a capital L are said to have 90 degrees, a flat line ___ has 180 degrees and flipping the whole thing over completes the circle with 270 degrees and finally 360.
Radians
Radians are ways of measuring angles as they are drawing inside a circle. If we take the circumference of a circle we get C = 2(pi), thus we can draw a unit circle (circle with circumference = 1) around any angle and be able to express the measure of that angle in terms of radians. Thus the L would become (Pi/2) or 1/4 the circumference, which also equates to 90 degrees. The flat line ___ would become Pi, or half the circle, this would equate to 180 degrees.
Friday, January 9, 2009
One to one functions (or injections)
A function f mapping the set A to the set B is said to be one to one, or an injection, if and only if (x,y) is in f and (z,y) is in f, implies that x=z.
Thursday, January 8, 2009
Onto functions (or surjections)
A function that maps to its codomain is called a surjection.
Consider the case a function f(n)=2n maps from the natural numbers to the set of real numbers. This would be considered a surjection since the mapping would only include the set of naturals anyway, and the codomain would be the same.
Consider the case a function f(n)=2n maps from the natural numbers to the set of real numbers. This would be considered a surjection since the mapping would only include the set of naturals anyway, and the codomain would be the same.
Wednesday, January 7, 2009
Let I be an interval of the real line prove that the following function decreases on that line
Let I be an interval of the real line, that is to say, let I be a line somewhere on the line from negative infinity to positive infinity. Also let I be a subset of the domain of g (a function). It can be said that g is decreasing on I if and only if for all x,y that is an element of I, if x < y then g(x) > g(y).
Prove that g is decreasing on the set of real numbers where g(x)= 2 - 5x
Suppose that x < y then 5x < 5y and therefore 2-5x > 2-5y, and thus g(x) > g(y), so f is decreasing on the interval I and the set of real numbers.
Prove that g is decreasing on the set of real numbers where g(x)= 2 - 5x
Suppose that x < y then 5x < 5y and therefore 2-5x > 2-5y, and thus g(x) > g(y), so f is decreasing on the interval I and the set of real numbers.
Tuesday, January 6, 2009
Let I be an interval of the real line prove that the following function increases on that line
Let I be an interval of the real line, that is to say, let I be a line somewhere on the line from negative infinity to positive infinity. Also let I be a subset of the domain of f (a function). It can be said that f is increasing on I if and only if for all x,y that is an element of I, if x < y then f(x) < f(y).
Prove that f is increasing on the set of real numbers where f(x)= 3x - 7
Suppose that x < y then 3x < 3y and therefore 3x-7 < 3y-7, and thus f(x) < f(y), so f is increasing on the interval I and the set of real numbers.
Prove that f is increasing on the set of real numbers where f(x)= 3x - 7
Suppose that x < y then 3x < 3y and therefore 3x-7 < 3y-7, and thus f(x) < f(y), so f is increasing on the interval I and the set of real numbers.
Monday, January 5, 2009
Prove that two functions f and g are equal if and only if...
Prove that two functions f and g are equal if and only if
1. The domain of f is equal to the domain of g
and
2. for all x that are elements of the domain of f, f(x)=g(x)
The domain simply refers to the first coordinate for all coordinates in the function.
Proof:
Assume f=g
1. Suppose that x is an element in the domain of f, then (x,y) is an element of f for some y. Since we assume that f=g then (x,y) is also an element of g and x must be an element in the domain of g. Thus the domain of f must be a subset of the domain of g, and similarly g must be a subset of f. So the two domains are equal.
2. Again suppose that x is an element of the domain of f. Then for some y, (x,y) is an element of f. Since f=g, (x,y) must also be an element of g. Therefore f(x)=y=g(x)
1. The domain of f is equal to the domain of g
and
2. for all x that are elements of the domain of f, f(x)=g(x)
The domain simply refers to the first coordinate for all coordinates in the function.
Proof:
Assume f=g
1. Suppose that x is an element in the domain of f, then (x,y) is an element of f for some y. Since we assume that f=g then (x,y) is also an element of g and x must be an element in the domain of g. Thus the domain of f must be a subset of the domain of g, and similarly g must be a subset of f. So the two domains are equal.
2. Again suppose that x is an element of the domain of f. Then for some y, (x,y) is an element of f. Since f=g, (x,y) must also be an element of g. Therefore f(x)=y=g(x)
Sunday, January 4, 2009
Step Functions
Step functions can be seen as generalizations of characteristic functions.
Step functions can be expressed as b = {b sub a such that a has multiple definitions)
For example consider a set M equal to a coordinate [1,5] expressed on multiple sets Bsub1=[1,2]
Bsub2=[2,4]
Bsub3=[4,5]
Now let all the sub numbers be defined on the y axis as follows
Ysub(1)=3
Ysub(2)=4
Ysub(3)=2
The resulting graph would be a series from 1 to 5 on the horizontal x axis (set A) with a line going from 1 to 2 at point 3 on the y axis, and another line going from 2 to 4 at point 4 on the y axis, and then another line completing the "step" to 5 from 4 to 5 at point 2 on the y axis.
Step functions can be expressed as b = {b sub a such that a has multiple definitions)
For example consider a set M equal to a coordinate [1,5] expressed on multiple sets Bsub1=[1,2]
Bsub2=[2,4]
Bsub3=[4,5]
Now let all the sub numbers be defined on the y axis as follows
Ysub(1)=3
Ysub(2)=4
Ysub(3)=2
The resulting graph would be a series from 1 to 5 on the horizontal x axis (set A) with a line going from 1 to 2 at point 3 on the y axis, and another line going from 2 to 4 at point 4 on the y axis, and then another line completing the "step" to 5 from 4 to 5 at point 2 on the y axis.
Labels:
Characteristic function,
functions,
set theory,
step function,
y axis
Saturday, January 3, 2009
Characteristic Functions
Characteristic functions define the functions of sets and the functions of all object outside the set.
Take for consideration the set A that is part of the Universe. Then the characteristic function can be seen as
f(x)={1 if x is an element of A, and 0 if x is an element of everything but A, (or U-A)}.
Take for consideration the set A that is part of the Universe. Then the characteristic function can be seen as
f(x)={1 if x is an element of A, and 0 if x is an element of everything but A, (or U-A)}.
Labels:
Characteristic function,
function,
functions,
universe
Friday, January 2, 2009
Constant Function
A constant function is a function with one codomain.
And example of this is the function f(x)=3
in set notation this would be
{(x,3) for all x that is an element of the real numbers}
as a graph it would look like a horizontal line where the vertical axis equals 3.
And example of this is the function f(x)=3
in set notation this would be
{(x,3) for all x that is an element of the real numbers}
as a graph it would look like a horizontal line where the vertical axis equals 3.
Labels:
codomain,
constant function,
functions,
set theory
Thursday, January 1, 2009
Ranges and Codomains
Ranges and Codomains
The domain of a function can be seen as the first coordinate of an ordered pair, and the range cam be seen as the second coordinate. Thus for the ordered pair (3,5) 3 is the domain, and 5 is the domain. Every function can only have one domain and one range. Even though functions can have many many ordered pairs.
There can be, however, many co domains, as long as the function is a subset of the codomain. Consider the example:
A = {4,5,6}
B = {2,5,7}
Then the following two sets are functions of A and B with different codomains.
f1={(4,2),(5,5),(6,7)}
f2={(4,5),(5,7),(6,5)}
The domain of a function can be seen as the first coordinate of an ordered pair, and the range cam be seen as the second coordinate. Thus for the ordered pair (3,5) 3 is the domain, and 5 is the domain. Every function can only have one domain and one range. Even though functions can have many many ordered pairs.
There can be, however, many co domains, as long as the function is a subset of the codomain. Consider the example:
A = {4,5,6}
B = {2,5,7}
Then the following two sets are functions of A and B with different codomains.
f1={(4,2),(5,5),(6,7)}
f2={(4,5),(5,7),(6,5)}
Subscribe to:
Posts (Atom)




