The Law of Sines

When we know the measure of the angles of a triangle, and the measure of one of its sides, we can use the law of sines to find the length of the other two sides.

The law sines states for any triangle with sides A,B, or C that
sin(a)/A = sin(b)/B = sin(c)/C
or equivalently
A/sin(a) = B/sin(b) = C/sin(c)

So if we have a triangle as such, with side x unknown we can find it by using the law of sines:


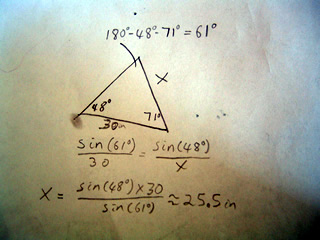
Proof of the Law of Sines
Consider the following diagram:


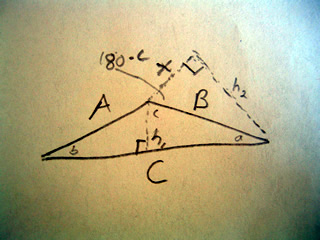
In the first step of the proof we divide the triangle into two right triangles by drawing a line of length h1.

Now we have two right triangles we can say that
sin(b)=h/A or h=A*sin(b)
similarly
sin(a)=h/B so h=B*sin(a)

now we can see that
B*sin(a)=h=A*sin(b)

divide both sides by AB and we get
sin(a)/A = sin(b)/B which is the first half of the law of sines.

For the next part, we draw a right triangle out from side B, creating a new length h2.

From this new triangle we see that
sin(b)=h/C and h=sin(b)*C
we also see that
sin(180-c) = h/B or h=sin(180-c)*B

but from the unit circle below we see that sin(180-c)=sin(c)


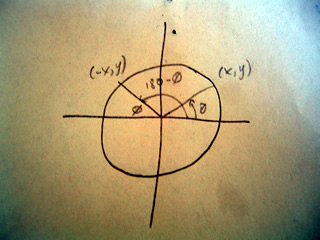
so we can write sin(c)*B=h and from this conclude
sin(b)*C=h=sin(c)*B
again we divide both sides by BC and get
sin(b)/B = sin(c)/C

so we have sin(a)/A=sin(b)/B=sin(c)/C which is the law of sines.