Prove that sin^2(x) + cos^2(x) = 1

Prove that sin^2(x) + cos^2(x) = 1



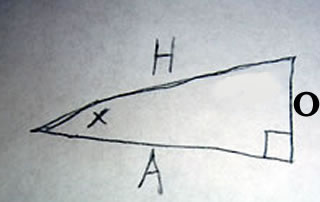
by Pythagorean Theorem A^2 + O^2 = H^2

Now, if we divide both sides by H^2 we get

(A^2 + O^2)/H^2 = H^2/H^2

which is

A^2/H^2 + O^2/H^2 = 1

which is

(A/H)^2 + (O/H)^2 = 1

now sin(x) = A/H and cos(x)=O/H so

sin^2(x) + cos^2(x) = 1