The Law of Cosines

When we know the length of two sides of a triangle, and the angle between them, we can use the law of cosines to find the length of the remaining side.

The law of cosines states:
C^2 = A^2 + B^2 - 2AB*cos(theta)

Here is an example of the law of cosines:


Proof of the Law of Cosines
The law of cosines looks similar to the pythagorean theorem (C^2 = A^2 + B^2) and indeed the two are similar. What we have to do to prove the law of cosines is to create a right triangle and define coordinates for that right triangle so we can find our remaining side.

Consider the diagram below:


Imagine the triangle on a coordinate plane. We define the origin, the point (0,0) at the end of side B. Thus the coordinate to the left is (-B,0). The coordinate at the top of the triangle (A*cos(theta)-B,A*sin(theta)) is derived from the right triangle sketch in on the right of our triangle. Although the coordinates appear complex, keep in mind they represent two numbers:
(A*cos(theta)-B,A*sin(theta)) is equal to some (x,y) on the coordinate plane.

Now that we have defined some coordinates we can draw a line down from the top angle to some point on side B, this creates a right triangle as shown below.


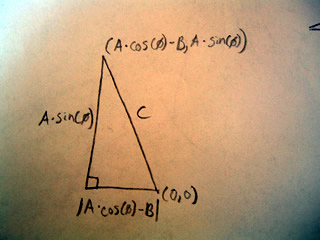
Using the coordinates which we defined we can define the length of the sides of this triangle.
The bottom side has length: |A*cos(theta)-B|.
A*cos(theta) comes from the dotted triangle we sketched in the previous image and represents the length that we have chopped off of side B. This the new length of the triangle is A*cos(theta)-B , it could also be B-A*cos(theta). Because we don't know which way to subtract, we take the absolute value so that both equations give us the same length, and write the distance as |A*cos(theta)-B|. The length of the vertical side also comes from the previous dotted triangle, and is simply A*sin(theta).

With these lengths now defined we can find C with the pythagorean theorem.
C²= (A*sin(theta)² + (A*cos(theta) - B)²
Mutliply this out and you get
C²=A²*sin²(theta) +A²cos²(theta) - 2AB*cos(theta) + B²
Factoring out the A² we get
C²=A²(sin²(theta)+cos²(theta))-2AB*cos(theta)+B²

Knowing that sin²(theta)+cos²(theta)=1 we get

C²=A² - 2AB*cos(theta) + B²

whic is the Law of Cosines.
C² = A² + B² - 2AB*cos(theta)