Proof of Herons Formula to find the area of a non-right triangle

Proof of Herons Formula to find the area of a non-right triangle

Consider the following triangle:


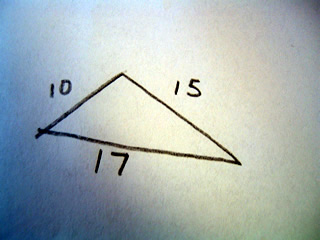
There are no right angles in the triangle, so therefore we must use Heron's forumla which first defines a variable s

s=1/2(a+b+c) where a,b,c each represent the length of a side.
then the area of the triangle is equal to
sqrt(s(s-a)(s-b)(s-c))

For the example we see that s=21
and the area is equal to
sqrt(21(21-10)(21-15)(21-17))
=
sqrt(21*11*6*4)=sqrt(5,544)=~74.46 which is the area of the triangle.

How do we prove Herons formula? Consider the triangle:


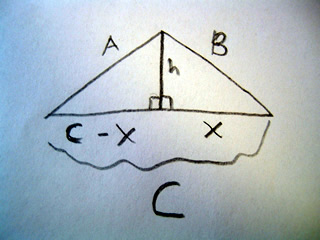
Here we have taken a triangle with no right angles, and cut a line so that we create two right triangles, and two new lengths at the base: x, and C-x. Now we need to solve for two unknown values x and h. We will solve for x first.

We can use pythagorean theorem to create equations for our new values, we see we have:

x² + h² = B²
and
(c-x)² + h² = A²
=
C² - 2cx + x²+ h² = A²

We know that B= x²+h² so we substitute that in to the equation above and get

C² - 2cx + B² = A²

Now we can solve for x!

x= (A² - B² - C²) / - 2c

Now we have x we can plug it back in to the equation

x² + h² = B²

thus

h = sqrt(B² - (A² - B² - C²) / - 2c)²)

Now, we know our base is equal to C and our height is equal to h, if we substitute these two values into the formula for the area of a triangle we get
(1/2)*b*h = 1/2*C²*sqrt(B² - (A² - B² - C²) / - 2c)²)

That is a complicated formula, so Heron found that you could define a term
s = (1/2)*( A + B + C) and then found the area formula could become a simpler

sqrt(s(s-a)(s-b)(s-c))

If you plug s in to the area formula above you will find the result we saw above:
1/2*C²*sqrt(B² - (A² - B² - C²) / - 2c)²)

which is the area of the triangle.