Prove that an isosceles right traingle has 45, 45, and 90 degree angles

Prove that an isosceles right triangle has 45, 45, and 90 degree angles.



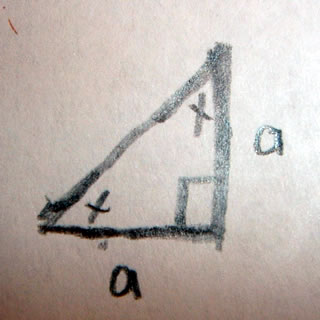
Remembering what we know about isosceles triangles we can find any two angles of a triangle if we know one angle.

Thus since we know one angle is equal to 90 degrees, the remaining two angles are equal to each other, and all the angles of a triangle must equal 180 degrees, we can say

2x + 90 = 180

solving we get x=45

Thus the angles are 45, 45, 90

or Pi/4 , Pi/4 , Pi/2 radians.

The Pythagorean theorem can be written as follows for isosceles right triangles
2a² = Hypotenuse²