Pythagorean Triples

Pythagorean Triples occur when right angled triangles contain whole numbered sides. In other words, when a,b, and c are whole numbers for the diagram below.



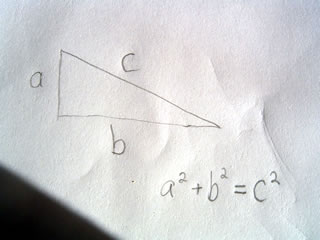
Thus if a=3 b=4 then c=5

We see 3^2 + 4^2 = 5^2 or 9 + 16 = 25

however, if b has a length of 5 (b=5) then we have

3^2 + 5^2 = 34 and the square root of 34 is 5.83095...
which isn't a whole number. Thus a right angled triangle with sides 3,4,5 is a Pythagorean triple, but a right angled triangle with sides 3,5,5.83095... isn't.

We can find Pythagorean triples (a,b,c) by taking any two whole number r and s, where r is greater than s (r > s)

then set
a= 2rs
b= r^2 - s^2
c= r^2 + s^2

As an example let r=5 and s=2
then
a=20
b=21
and
c=29

we see it is a Pythagorean triple because 20^2 + 21^2 = 29^2

or 400 + 441= 841

We can see how it works by plugging in the values for a and b.

Thus
a^2 + b^2 =

(2rs)^2 + (r^2 - s^2)^2 =

4(r^2)(s^2) + r^4 - 2(r^2)(s^2) + s^4 =

r^4 + 2(r^2)(s^2) + s^4 =

(r^2 + s^2)^2 = c^2

Thus

a^2 + b^2 = c^2