Arcfunctions, or inverse functions, of trigonometry allow you to find the degree of an angle if you have the ratios.
Thus arcsin(1/2) = 30 degrees
since sin(30) = 1/2
this can also be written as
sin-1(1/2) = 30 degrees
The arc functions can produce more than one value, for example
arcsin(sqrt2/2) can equal 90 degrees and 135 degrees.
As we learned when we covered functions in set theory, functions can be defined on any domain, and thus, the arc functions are defined to be between -90 and 90 degrees to avoid getting more than one output. That is -Pi/2 and Pi/2 radians.
Saturday, January 31, 2009
Friday, January 30, 2009
The Sine function And Circles
Yesterday we learned that sine is the y coordinate of any point on the unit circle. Thus if we take the circumference of the circle and place it on the x-axis from 0 to 2pi, we can evaluate sin at any point. The result is the graph that represent a stretched out circle.

Graph from wikipedia.
The curve of a circle occurs many places in nature and is used to model frequencies of energy, such as electricity and sound.

Graph from wikipedia.
The curve of a circle occurs many places in nature and is used to model frequencies of energy, such as electricity and sound.
Thursday, January 29, 2009
Prove that the coordinates of a particular angle on the unit circle are the cosine and sine of that angle.
Prove that the coordinates of a particular angle on the unit circle are the cosine and sine of that angle.
Consider the unit circle with coordinates x and y:
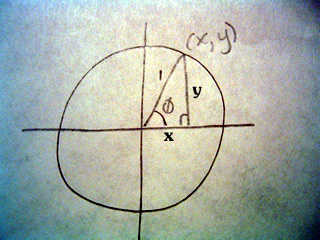
Cosine is defined as the side adjacent to the angle divided by the hypotenuse, (A/H), or in this case (x/1) so we see that cosine = x
Similarly sine is defined as the side opposite the angle divided by the hypotenuse, (O/H), or in this case (y/1) so we see that sine = 1
Thus we have proved that the coordinates of a particular angle on the unit circle are the cosine and sine of that angle, as shown below:

Consider the unit circle with coordinates x and y:

Cosine is defined as the side adjacent to the angle divided by the hypotenuse, (A/H), or in this case (x/1) so we see that cosine = x
Similarly sine is defined as the side opposite the angle divided by the hypotenuse, (O/H), or in this case (y/1) so we see that sine = 1
Thus we have proved that the coordinates of a particular angle on the unit circle are the cosine and sine of that angle, as shown below:

Wednesday, January 28, 2009
Finding coordinates on the Unit Circle
Coordinates can be found on the unit circle by inscribing 60, 45, and 30 degree triangles.
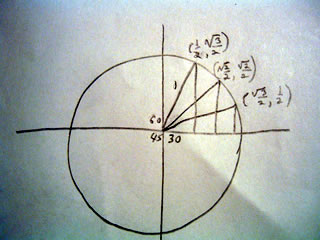
Thus triangles with
60 degrees corresponds to the coordinate (1/2,sqrt(3)/2)
45 degrees corresponds to the coordinate (sqrt(2)/2,sqrt(2)/2)
30 degrees corresponds to the coordinate (sqrt(3)/2,1/2)
So the adjacent side makes the x axis, the opposite side makes the y axis, and the hypotenuse always equals 1.

Thus triangles with
60 degrees corresponds to the coordinate (1/2,sqrt(3)/2)
45 degrees corresponds to the coordinate (sqrt(2)/2,sqrt(2)/2)
30 degrees corresponds to the coordinate (sqrt(3)/2,1/2)
So the adjacent side makes the x axis, the opposite side makes the y axis, and the hypotenuse always equals 1.
Labels:
coordinates,
trigonemtry,
unit circle coordinates
Tuesday, January 27, 2009
Unit Circle and Sample Angles
The unit circle is a circle with radius 1 and is used to evaluate trigonometric functions.
The unit circle can tell us the measure of any angle from the origin to an (x,y) coordinate, however, angles can be more than 360 degrees on the circle, as we see in the example.
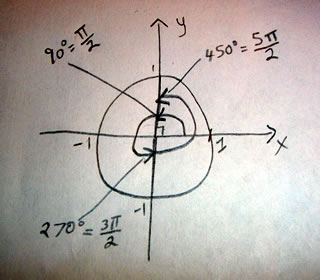
Thus at point (0,1) we have both
90 degrees or (Pi/2)
and
450 degrees or (5pi/2)
at point
(0,-1) we have 270 degrees or (3Pi/2)
Thus we see how the unit circle is used to measure angles, we will see in future posts how it relates to the trigonometric functions.
The unit circle can tell us the measure of any angle from the origin to an (x,y) coordinate, however, angles can be more than 360 degrees on the circle, as we see in the example.

Thus at point (0,1) we have both
90 degrees or (Pi/2)
and
450 degrees or (5pi/2)
at point
(0,-1) we have 270 degrees or (3Pi/2)
Thus we see how the unit circle is used to measure angles, we will see in future posts how it relates to the trigonometric functions.
Monday, January 26, 2009
Right Triangles in Equilateral Triangle
Equilateral triangles do not have right angles, making them difficult to work with in regards to trigonometric equations. This can be solved by cutting the triangle in half, thus creating two triangles.
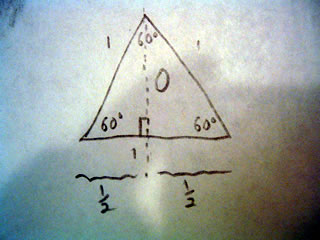
From the triangle above, we can find the length of the dotted line, 0, by pythagorean theorem.
This (1/2)2 + O2 = 12
=
(1/4) + O2 = 1
O = Sqrt(1-(1/4)) = sqrt(3/4) = sqrt(3)/2
The new angle at the top of the triangle can also be found, since all angles add up to 180, we get:
60 + y + 90 = 180
and so y=30 , exactly half of 60.
in degrees this is 30*(pi/180) = Pi/6

From the triangle above, we can find the length of the dotted line, 0, by pythagorean theorem.
This (1/2)2 + O2 = 12
=
(1/4) + O2 = 1
O = Sqrt(1-(1/4)) = sqrt(3/4) = sqrt(3)/2
The new angle at the top of the triangle can also be found, since all angles add up to 180, we get:
60 + y + 90 = 180
and so y=30 , exactly half of 60.
in degrees this is 30*(pi/180) = Pi/6
Sunday, January 25, 2009
Prove that an isosceles right traingle has 45, 45, and 90 degree angles
Prove that an isosceles right triangle has 45, 45, and 90 degree angles.
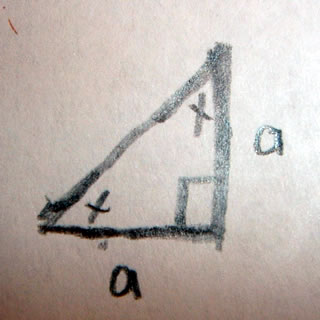
Remembering what we know about isosceles triangles we can find any two angles of a triangle if we know one angle.
Thus since we know one angle is equal to 90 degrees, the remaining two angles are equal to each other, and all the angles of a triangle must equal 180 degrees, we can say
2x + 90 = 180
solving we get x=45
Thus the angles are 45, 45, 90
or Pi/4 , Pi/4 , Pi/2 radians.
The Pythagorean theorem can be written as follows for isosceles right triangles
2a2 = Hypotenuse2
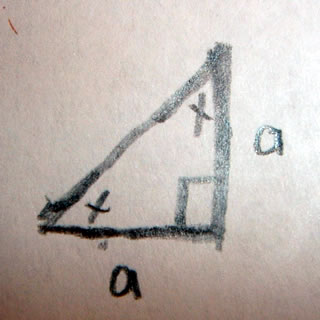
Remembering what we know about isosceles triangles we can find any two angles of a triangle if we know one angle.
Thus since we know one angle is equal to 90 degrees, the remaining two angles are equal to each other, and all the angles of a triangle must equal 180 degrees, we can say
2x + 90 = 180
solving we get x=45
Thus the angles are 45, 45, 90
or Pi/4 , Pi/4 , Pi/2 radians.
The Pythagorean theorem can be written as follows for isosceles right triangles
2a2 = Hypotenuse2
Saturday, January 24, 2009
Prove that tan2(x) + 1 = sec2(x)
Prove that tan2(x) + 1 = sec2(x)
We know that
sin2(x) + cos2(x) = 1
dividing both sides by cos2(x) we get
(sin2(x) + cos2(x))/cos2(x) = 1/cos2(x)
which equals
sin2(x)/cos2(x) + cos2(x)/cos2(x) = (1/cos(x))2
which can be re-written as
(sin(x)/(cos(x))2 + 1 = (1/cos(x))2
We know that tan2(x) = (sin(x)/(cos(x))2
and that (1/cos(x))2 = sec2(x)
So we can write
cot2(x) + 1 = sec2(x)
We know that
sin2(x) + cos2(x) = 1
dividing both sides by cos2(x) we get
(sin2(x) + cos2(x))/cos2(x) = 1/cos2(x)
which equals
sin2(x)/cos2(x) + cos2(x)/cos2(x) = (1/cos(x))2
which can be re-written as
(sin(x)/(cos(x))2 + 1 = (1/cos(x))2
We know that tan2(x) = (sin(x)/(cos(x))2
and that (1/cos(x))2 = sec2(x)
So we can write
cot2(x) + 1 = sec2(x)
Friday, January 23, 2009
Prove that sin^2(x) + cos^2(x) = 1
Prove that sin^2(x) + cos^2(x) = 1
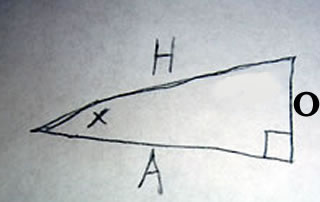
by Pythagorean Theorem A^2 + O^2 = H^2
Now, if we divide both sides by H^2 we get
(A^2 + O^2)/H^2 = H^2/H^2
which is
A^2/H^2 + O^2/H^2 = 1
which is
(A/H)^2 + (O/H)^2 = 1
now sin(x) = A/H and cos(x)=O/H so
sin^2(x) + cos^2(x) = 1

by Pythagorean Theorem A^2 + O^2 = H^2
Now, if we divide both sides by H^2 we get
(A^2 + O^2)/H^2 = H^2/H^2
which is
A^2/H^2 + O^2/H^2 = 1
which is
(A/H)^2 + (O/H)^2 = 1
now sin(x) = A/H and cos(x)=O/H so
sin^2(x) + cos^2(x) = 1
Thursday, January 22, 2009
Secant, cosecant, and cotangent.
After sine, cosine, and tangent, there are only 3 more possible ratios to be made from a triangle. These last relations are the inverse of the respective functions, they are secant (sec), cosecant (csc), and cotangent (cot).

x = The angle x
O = Opposite side of the angle x
A = Adjacent side of the angle x
H = Hypotenuse
sin(x) = O/H
csc(x) = H/O
cos(x) = A/H
sec(x) = H/A
tan(x) = O/A
cot(x) = A/O

x = The angle x
O = Opposite side of the angle x
A = Adjacent side of the angle x
H = Hypotenuse
sin(x) = O/H
csc(x) = H/O
cos(x) = A/H
sec(x) = H/A
tan(x) = O/A
cot(x) = A/O
Wednesday, January 21, 2009
Prove that tan(x) = sin(x)/cos(x)
Prove that tan(x) = sin(x)/cos(x)

sin(x) = (0/H)
cos(x) = (A/H)
Then sin(x)/cos(x) =
(O/H)/(A/H) =
(O/H)*(H/A) =
(O/A) = tan(x)
So sin(x)/cos(x) = tan(x)

sin(x) = (0/H)
cos(x) = (A/H)
Then sin(x)/cos(x) =
(O/H)/(A/H) =
(O/H)*(H/A) =
(O/A) = tan(x)
So sin(x)/cos(x) = tan(x)
Labels:
cool proofs,
cosine,
sine,
tangent,
trigonomentric proofs
Tuesday, January 20, 2009
Tangent
The tangent function is defined as the length of the side opposite the angle x divided by the length of the adjacent angle.
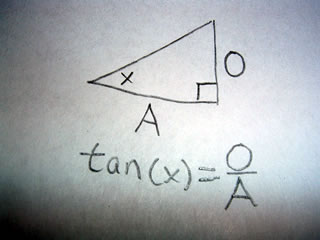
Thus if O=5 and A=3 then
tan(x)=5/3
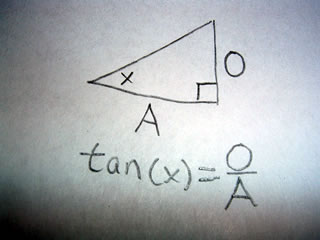
Thus if O=5 and A=3 then
tan(x)=5/3
Monday, January 19, 2009
A relationship between sine and cosine
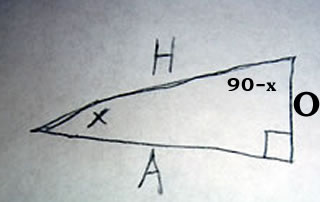
From the figure above the cosine of x can be defined as follows:
cos(x) = sin(90 - x)
This is because we know we have one 90 degree angle, a right angle, so the other two angles must equal 90 degrees, since the interior angles of a triangle always add up to 180 degrees. When the measure of two angles are dependent on each other in this way they can be called complements,. The name cosine originated this way, since it is the compliment of sine.
Sunday, January 18, 2009
Cosine
The cosine of an angle can be defined as the length of the adjacent side divided by the length of the hypotenuse.

This if A=4 and H=9 then
cos(x) = (4/9)

This if A=4 and H=9 then
cos(x) = (4/9)
Saturday, January 17, 2009
Sine: The first trigonometric function
The sine of an angle is defined as the length of the hypotenuse divided by the length of the opposite side.
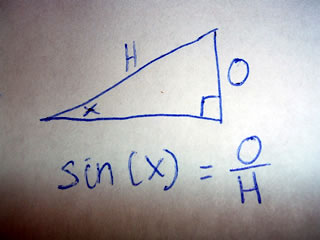
Thus if O=6 and H=10 then
sin(x) = 6/10
= 3/5
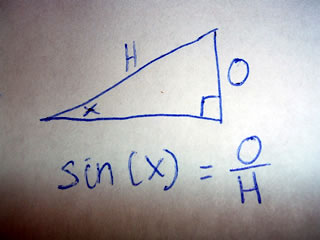
Thus if O=6 and H=10 then
sin(x) = 6/10
= 3/5
Friday, January 16, 2009
Pythagorean Triples
Pythagorean Triples occur when right angled triangles contain whole numbered sides. In other words, when a,b, and c are whole numbers for the diagram below.
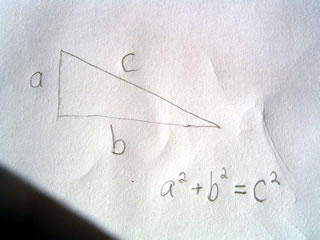
Thus if a=3 b=4 then c=5
We see 3^2 + 4^2 = 5^2 or 9 + 16 = 25
however, if b has a length of 5 (b=5) then we have
3^2 + 5^2 = 34 and the square root of 34 is 5.83095...
which isn't a whole number. Thus a right angled triangle with sides 3,4,5 is a Pythagorean triple, but a right angled triangle with sides 3,5,5.83095... isn't.
We can find Pythagorean triples (a,b,c) by taking any two whole number r and s, where r is greater than s (r > s)
then set
a= 2rs
b= r^2 - s^2
c= r^2 + s^2
As an example let r=5 and s=2
then
a=20
b=21
and
c=29
we see it is a Pythagorean triple because 20^2 + 21^2 = 29^2
or 400 + 441= 841
We can see how it works by plugging in the values for a and b.
Thus
a^2 + b^2 =
(2rs)^2 + (r^2 - s^2)^2 =
4(r^2)(s^2) + r^4 - 2(r^2)(s^2) + s^4 =
r^4 + 2(r^2)(s^2) + s^4 =
(r^2 + s^2)^2 = c^2
Thus
a^2 + b^2 = c^2
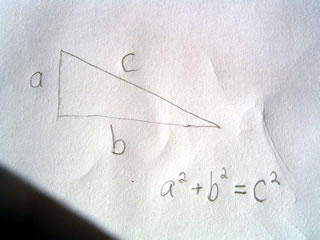
Thus if a=3 b=4 then c=5
We see 3^2 + 4^2 = 5^2 or 9 + 16 = 25
however, if b has a length of 5 (b=5) then we have
3^2 + 5^2 = 34 and the square root of 34 is 5.83095...
which isn't a whole number. Thus a right angled triangle with sides 3,4,5 is a Pythagorean triple, but a right angled triangle with sides 3,5,5.83095... isn't.
We can find Pythagorean triples (a,b,c) by taking any two whole number r and s, where r is greater than s (r > s)
then set
a= 2rs
b= r^2 - s^2
c= r^2 + s^2
As an example let r=5 and s=2
then
a=20
b=21
and
c=29
we see it is a Pythagorean triple because 20^2 + 21^2 = 29^2
or 400 + 441= 841
We can see how it works by plugging in the values for a and b.
Thus
a^2 + b^2 =
(2rs)^2 + (r^2 - s^2)^2 =
4(r^2)(s^2) + r^4 - 2(r^2)(s^2) + s^4 =
r^4 + 2(r^2)(s^2) + s^4 =
(r^2 + s^2)^2 = c^2
Thus
a^2 + b^2 = c^2
Thursday, January 15, 2009
The Pythagorean Theorem
The Pythagorean Theorem is probably the most well known theorem in trigonometry. It states that the sum of the squares of the sides of a right angle triangle is equal to the square of the hypotenuse.
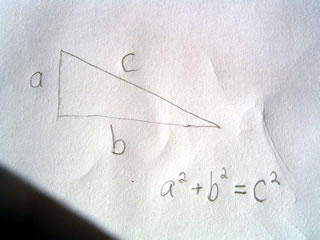
The proof of this theorem can be seen by making a square from four traingles. In the square it becomes evident that a^2 + b^2 = c^2

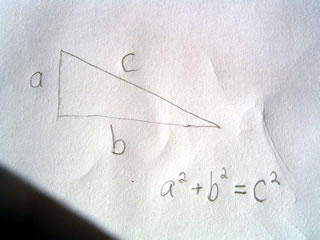
The proof of this theorem can be seen by making a square from four traingles. In the square it becomes evident that a^2 + b^2 = c^2

Wednesday, January 14, 2009
Scaling
Scaling of triangles occurs when one triangle is a copy of another triangle but has the length of its sized increased by some fixed factor x. In the example below we see two triangles. The second triangle is an enlarged version of the first triangle, and thus has been scaled up.
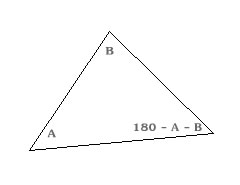
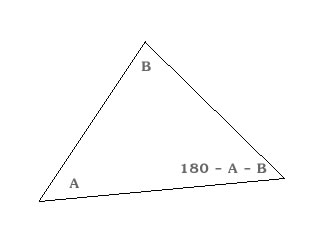
An interested property of scaled triangles is that the lengths of interior angles remains the same, no matter how large the triangle gets. You could have a triangle the size of the universe, and it would still have the same angle lengths.
Another interesting aspect is that if we know the length of any two similar sides we can calculate the scaling factor. Thus if the first triangle has a side with length 2 and the second a side with length 6, then we can say the scaling factor is 3. We can use this scaling factor to discern the lengths of the remaining sides of the larger triangle.


An interested property of scaled triangles is that the lengths of interior angles remains the same, no matter how large the triangle gets. You could have a triangle the size of the universe, and it would still have the same angle lengths.
Another interesting aspect is that if we know the length of any two similar sides we can calculate the scaling factor. Thus if the first triangle has a side with length 2 and the second a side with length 6, then we can say the scaling factor is 3. We can use this scaling factor to discern the lengths of the remaining sides of the larger triangle.
Tuesday, January 13, 2009
Isosceles and Equilateral Triangles
Isosceles triangles are triangles with two sides of equal length. Therefore if we know the measure of one angle we can calculate the measure of the remaining angles. If we know that the measure of the unequal angle is 30 degrees we can deduce that the remaining angles must each equal 75 degrees.
Let x equal the measure of our two equal angles. This 2x + 30 must equal 180, or the total measure of degrees in a triangle.
2x + 30 = 180
2x=150
x=75
Equilateral triangles are triangles which have sides of equal length and therefore angles of equal length. The angles of an equilateral triangle will always equal 60 degrees or (pi)/3 radians.
Let x equal the measure of our two equal angles. This 2x + 30 must equal 180, or the total measure of degrees in a triangle.
2x + 30 = 180
2x=150
x=75
Equilateral triangles are triangles which have sides of equal length and therefore angles of equal length. The angles of an equilateral triangle will always equal 60 degrees or (pi)/3 radians.
Monday, January 12, 2009
Prove that the interior angles of a triangle always add up to 180 degrees
Prove that the interior angles of a triangle always add up to 180 degrees.
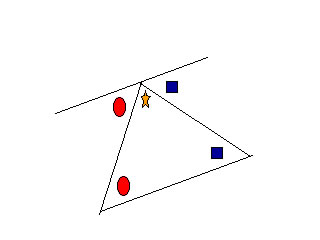
In the drawing above the angles of the circles are equal and the angles of the squares are equal by properties of geometry.
Thus we can see that: circle + star + square = 180 degrees, or Pi Radians, since all 3 angles form a straight line.
We can use this fact to calculate the length of any angle in a triangle if we know the length of the other two angles.
Thus if
Angle 1 = 40 degrees
Angle 2 = 60 degrees
then angle 3 must equal 80 degrees to complete the sum of angles to 180 degrees.
similarly if
Angle 1 = Pi/4 radians
Angle 2 = Pi/4 radians
then Angle 3 must be equal to Pi/2 radians to complete the sum of angles to Pi.

In the drawing above the angles of the circles are equal and the angles of the squares are equal by properties of geometry.
Thus we can see that: circle + star + square = 180 degrees, or Pi Radians, since all 3 angles form a straight line.
We can use this fact to calculate the length of any angle in a triangle if we know the length of the other two angles.
Thus if
Angle 1 = 40 degrees
Angle 2 = 60 degrees
then angle 3 must equal 80 degrees to complete the sum of angles to 180 degrees.
similarly if
Angle 1 = Pi/4 radians
Angle 2 = Pi/4 radians
then Angle 3 must be equal to Pi/2 radians to complete the sum of angles to Pi.
Sunday, January 11, 2009
Converting Degrees to Radians and Radians to Degrees
Yesterday we learned about degrees and radians: two ways to measure an angle.
Today we will learn how to convert one measure to the other.
A full circle is equal to 360 degrees which is equal to 2(pi)
Thus 360 degrees = 2(pi) radians
dividing by 360 we get
1 degree = 2(pi)/360
or
1 degree = (pi)/180
conversely
1 radian = 180/(pi) degrees
Examples
How many radians equal 150 degrees?
To find this we multiply by pi/180 thus
150*(pi/180) = 5(pi)/6 radians
So 150 degrees equals 5(pi)/6 radians. Radians are typically written as fractions since pi is irrational. Irrational means it has an infinite number of decimals.
---------------
Now let us convert radians to degrees, how many degrees are in 7(pi)/12 radians?
To find this we multiply the radians by 180/pi and so we get
7(pi)/12 * 180/pi = 105 degrees
So there are 105 degrees in 7(pi)/12 radians.
Today we will learn how to convert one measure to the other.
A full circle is equal to 360 degrees which is equal to 2(pi)
Thus 360 degrees = 2(pi) radians
dividing by 360 we get
1 degree = 2(pi)/360
or
1 degree = (pi)/180
conversely
1 radian = 180/(pi) degrees
Examples
How many radians equal 150 degrees?
To find this we multiply by pi/180 thus
150*(pi/180) = 5(pi)/6 radians
So 150 degrees equals 5(pi)/6 radians. Radians are typically written as fractions since pi is irrational. Irrational means it has an infinite number of decimals.
---------------
Now let us convert radians to degrees, how many degrees are in 7(pi)/12 radians?
To find this we multiply the radians by 180/pi and so we get
7(pi)/12 * 180/pi = 105 degrees
So there are 105 degrees in 7(pi)/12 radians.
Saturday, January 10, 2009
Trigonometry: Degrees and Radians
I have decided to take up reviewing trigonometry as a goal for this blog. In the first look at trigonometry it is necessary to understand angles. Angles are create by the intersection of two lines. They can be measured in degrees or radians.
Degrees
There are 360 degrees in any possible angle, the widest angle forming a complete circle. The number 360 was chosen by the Babylonians who counted in groups of 60 (base 60) where as we count in groups of 10 (base 10). Thus 1/60th of a degree is called a minute and 1/60th of a minute is called a second. This terminology is still used by navigators today, but some also use decimals. In any case, two perpendicular lines, like in a capital L are said to have 90 degrees, a flat line ___ has 180 degrees and flipping the whole thing over completes the circle with 270 degrees and finally 360.
Radians
Radians are ways of measuring angles as they are drawing inside a circle. If we take the circumference of a circle we get C = 2(pi), thus we can draw a unit circle (circle with circumference = 1) around any angle and be able to express the measure of that angle in terms of radians. Thus the L would become (Pi/2) or 1/4 the circumference, which also equates to 90 degrees. The flat line ___ would become Pi, or half the circle, this would equate to 180 degrees.
Degrees
There are 360 degrees in any possible angle, the widest angle forming a complete circle. The number 360 was chosen by the Babylonians who counted in groups of 60 (base 60) where as we count in groups of 10 (base 10). Thus 1/60th of a degree is called a minute and 1/60th of a minute is called a second. This terminology is still used by navigators today, but some also use decimals. In any case, two perpendicular lines, like in a capital L are said to have 90 degrees, a flat line ___ has 180 degrees and flipping the whole thing over completes the circle with 270 degrees and finally 360.
Radians
Radians are ways of measuring angles as they are drawing inside a circle. If we take the circumference of a circle we get C = 2(pi), thus we can draw a unit circle (circle with circumference = 1) around any angle and be able to express the measure of that angle in terms of radians. Thus the L would become (Pi/2) or 1/4 the circumference, which also equates to 90 degrees. The flat line ___ would become Pi, or half the circle, this would equate to 180 degrees.
Friday, January 9, 2009
One to one functions (or injections)
A function f mapping the set A to the set B is said to be one to one, or an injection, if and only if (x,y) is in f and (z,y) is in f, implies that x=z.
Thursday, January 8, 2009
Onto functions (or surjections)
A function that maps to its codomain is called a surjection.
Consider the case a function f(n)=2n maps from the natural numbers to the set of real numbers. This would be considered a surjection since the mapping would only include the set of naturals anyway, and the codomain would be the same.
Consider the case a function f(n)=2n maps from the natural numbers to the set of real numbers. This would be considered a surjection since the mapping would only include the set of naturals anyway, and the codomain would be the same.
Wednesday, January 7, 2009
Let I be an interval of the real line prove that the following function decreases on that line
Let I be an interval of the real line, that is to say, let I be a line somewhere on the line from negative infinity to positive infinity. Also let I be a subset of the domain of g (a function). It can be said that g is decreasing on I if and only if for all x,y that is an element of I, if x < y then g(x) > g(y).
Prove that g is decreasing on the set of real numbers where g(x)= 2 - 5x
Suppose that x < y then 5x < 5y and therefore 2-5x > 2-5y, and thus g(x) > g(y), so f is decreasing on the interval I and the set of real numbers.
Prove that g is decreasing on the set of real numbers where g(x)= 2 - 5x
Suppose that x < y then 5x < 5y and therefore 2-5x > 2-5y, and thus g(x) > g(y), so f is decreasing on the interval I and the set of real numbers.
Tuesday, January 6, 2009
Let I be an interval of the real line prove that the following function increases on that line
Let I be an interval of the real line, that is to say, let I be a line somewhere on the line from negative infinity to positive infinity. Also let I be a subset of the domain of f (a function). It can be said that f is increasing on I if and only if for all x,y that is an element of I, if x < y then f(x) < f(y).
Prove that f is increasing on the set of real numbers where f(x)= 3x - 7
Suppose that x < y then 3x < 3y and therefore 3x-7 < 3y-7, and thus f(x) < f(y), so f is increasing on the interval I and the set of real numbers.
Prove that f is increasing on the set of real numbers where f(x)= 3x - 7
Suppose that x < y then 3x < 3y and therefore 3x-7 < 3y-7, and thus f(x) < f(y), so f is increasing on the interval I and the set of real numbers.
Monday, January 5, 2009
Prove that two functions f and g are equal if and only if...
Prove that two functions f and g are equal if and only if
1. The domain of f is equal to the domain of g
and
2. for all x that are elements of the domain of f, f(x)=g(x)
The domain simply refers to the first coordinate for all coordinates in the function.
Proof:
Assume f=g
1. Suppose that x is an element in the domain of f, then (x,y) is an element of f for some y. Since we assume that f=g then (x,y) is also an element of g and x must be an element in the domain of g. Thus the domain of f must be a subset of the domain of g, and similarly g must be a subset of f. So the two domains are equal.
2. Again suppose that x is an element of the domain of f. Then for some y, (x,y) is an element of f. Since f=g, (x,y) must also be an element of g. Therefore f(x)=y=g(x)
1. The domain of f is equal to the domain of g
and
2. for all x that are elements of the domain of f, f(x)=g(x)
The domain simply refers to the first coordinate for all coordinates in the function.
Proof:
Assume f=g
1. Suppose that x is an element in the domain of f, then (x,y) is an element of f for some y. Since we assume that f=g then (x,y) is also an element of g and x must be an element in the domain of g. Thus the domain of f must be a subset of the domain of g, and similarly g must be a subset of f. So the two domains are equal.
2. Again suppose that x is an element of the domain of f. Then for some y, (x,y) is an element of f. Since f=g, (x,y) must also be an element of g. Therefore f(x)=y=g(x)
Sunday, January 4, 2009
Step Functions
Step functions can be seen as generalizations of characteristic functions.
Step functions can be expressed as b = {b sub a such that a has multiple definitions)
For example consider a set M equal to a coordinate [1,5] expressed on multiple sets Bsub1=[1,2]
Bsub2=[2,4]
Bsub3=[4,5]
Now let all the sub numbers be defined on the y axis as follows
Ysub(1)=3
Ysub(2)=4
Ysub(3)=2
The resulting graph would be a series from 1 to 5 on the horizontal x axis (set A) with a line going from 1 to 2 at point 3 on the y axis, and another line going from 2 to 4 at point 4 on the y axis, and then another line completing the "step" to 5 from 4 to 5 at point 2 on the y axis.
Step functions can be expressed as b = {b sub a such that a has multiple definitions)
For example consider a set M equal to a coordinate [1,5] expressed on multiple sets Bsub1=[1,2]
Bsub2=[2,4]
Bsub3=[4,5]
Now let all the sub numbers be defined on the y axis as follows
Ysub(1)=3
Ysub(2)=4
Ysub(3)=2
The resulting graph would be a series from 1 to 5 on the horizontal x axis (set A) with a line going from 1 to 2 at point 3 on the y axis, and another line going from 2 to 4 at point 4 on the y axis, and then another line completing the "step" to 5 from 4 to 5 at point 2 on the y axis.
Labels:
Characteristic function,
functions,
set theory,
step function,
y axis
Saturday, January 3, 2009
Characteristic Functions
Characteristic functions define the functions of sets and the functions of all object outside the set.
Take for consideration the set A that is part of the Universe. Then the characteristic function can be seen as
f(x)={1 if x is an element of A, and 0 if x is an element of everything but A, (or U-A)}.
Take for consideration the set A that is part of the Universe. Then the characteristic function can be seen as
f(x)={1 if x is an element of A, and 0 if x is an element of everything but A, (or U-A)}.
Labels:
Characteristic function,
function,
functions,
universe
Friday, January 2, 2009
Constant Function
A constant function is a function with one codomain.
And example of this is the function f(x)=3
in set notation this would be
{(x,3) for all x that is an element of the real numbers}
as a graph it would look like a horizontal line where the vertical axis equals 3.
And example of this is the function f(x)=3
in set notation this would be
{(x,3) for all x that is an element of the real numbers}
as a graph it would look like a horizontal line where the vertical axis equals 3.
Labels:
codomain,
constant function,
functions,
set theory
Thursday, January 1, 2009
Ranges and Codomains
Ranges and Codomains
The domain of a function can be seen as the first coordinate of an ordered pair, and the range cam be seen as the second coordinate. Thus for the ordered pair (3,5) 3 is the domain, and 5 is the domain. Every function can only have one domain and one range. Even though functions can have many many ordered pairs.
There can be, however, many co domains, as long as the function is a subset of the codomain. Consider the example:
A = {4,5,6}
B = {2,5,7}
Then the following two sets are functions of A and B with different codomains.
f1={(4,2),(5,5),(6,7)}
f2={(4,5),(5,7),(6,5)}
The domain of a function can be seen as the first coordinate of an ordered pair, and the range cam be seen as the second coordinate. Thus for the ordered pair (3,5) 3 is the domain, and 5 is the domain. Every function can only have one domain and one range. Even though functions can have many many ordered pairs.
There can be, however, many co domains, as long as the function is a subset of the codomain. Consider the example:
A = {4,5,6}
B = {2,5,7}
Then the following two sets are functions of A and B with different codomains.
f1={(4,2),(5,5),(6,7)}
f2={(4,5),(5,7),(6,5)}
Subscribe to:
Comments (Atom)



