For example, assume we took a sample survey and found that 80% of the population preferred cheese to wine. We can make a more accurate statement if we say that there is a 95% chance that between 77% and 83% of the population prefers cheese to wine.
This can also be reported as 80% of people prefer cheese to wine with a 3% margin of error.
How do we calculate this?
Well we need three things, the mean(u) the standard error (H) and the Z-statistic from the normal curve (Z)
What is the Z statistic? Well consider the graph below:
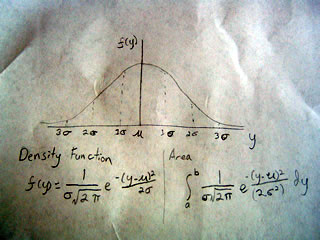
Suppose we wanted to find the point on the curve that would include 95% of the area. As this happens it is at the point (2 sigma) and the value of the x axis at this point is 1.96 That is to say when x equals 1.96 we capture 95% of the population under the curve. So the Z statistic equals that point on the x-axis or 1.96
Some other common levels of confidence and Z stats are
90% z=1.645
95% z=1.96
98% z=2.33
99% z=2.58
As you see, the Z statistic gets larger and larger as confidence increases. In other words we can be
95% sure that between 77-83% of people prefer wine to cheese
99% sure that between 76-84% of people prefer wine to cheese
and
100% sure that between 0-100% of people prefer wine to cheese (which isn't really saying anything at all)
Now for our example, the mean is 80% and assume the standard error is 1.5% (pretty small really)
to get our confidence interval we take the mean and add the Z stat times the standard error:
u + Z(H) upper limit
u - Z(H) lower limit
80 + 1.96(1.5) upper limit = 80 + 2.94 = 82.94 or rounded to 83%
80 - 1.96(1.5) lower limit = 80 - 2.94 = 77.06 or rounded to 77%
Thus we say with 95% confidence that the mean(u) is
77% < = u < = 83%
Because the mean is 80% we can find the margin of error by subtracting from the top interval.
83%-80% = 3 percent margin of error. Thus we make the statement 80% of people prefer wine to cheese with a 3% margin of error.




No comments:
Post a Comment